profile photo

Guía 5 - Impulso Lineal


hero image
Publicado el

Impulso lineal - Cantidad de movimiento

En física, la cantidad de movimiento se define como la multiplicación de la masa de un objeto por su velocidad, ósea p⃗=mv⃗\vec p = m \vec v. Para dejar clara su definición valdría la pena relacionar la cantidad de movimiento con la segunda ley de Newton.

∑F⃗=ma⃗=mdv⃗dt=d(mv⃗)dt=dp⃗dt\begin{split} \sum \vec F &= m\vec a\\ &= m \frac{d\vec v}{dt}\\ &= \frac{d(m\vec v)}{dt}\\ &= \frac{d\vec p}{dt} \end{split}

Es muy importante que prestemos atención a la expresión ∑F⃗=dp⃗dt\sum \vec F = \frac{d\vec p}{dt} porque nos indica como una resultante de fuerzas puede generar una cambio en la cantidad de movimiento de un cuerpo en una determinado tiempo.

Dicho esto, podemos decir que la cantidad de movimiento de un cuerpo es una característica de la dinámica del cuerpo en un momento determinado y que solo se puede ver perturbada por la aparición de fuerzas externas.

Ley de conservación del impulso lineal

Para que la cantidad de movimiento ser conserve, es preciso que dp⃗dt=0\frac{d\vec p}{dt}=0, lo que implica que la cantidad de movimiento de un cuerpo es constante o lo como se menciono anteriormente, si ninguna fuerza resultante perturba al cuerpo, entonces ∑F⃗=0\sum \vec F = 0.

Esto puede sonar hasta trivial para cuerpos puntuales, pero su aplicación se intensifica con la aparición de sistemas de partículas.

Consideremos por un el momento un sistema SS, formado por dos sub sistemas S1,S2S_1, S_2 que interactúan entre ellas. El sistema SS es un sistema aislado, donde ∑F⃗externas=0\sum \vec F_{\text{externas}} = 0, y donde las únicas fuerzas existentes son las que actúan en la interacción entre S1,S2S_1, S_2.

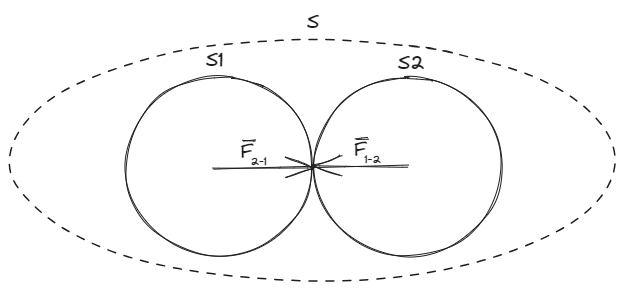
Untitled

Por la tercer ley de Newton, sabemos que las fuerzas F⃗2−1,F⃗1−2\vec F_{2-1}, \vec F_{1-2} son iguales en magnitud y contrarias vectorialmente, ósea F⃗2−1=−F⃗1−2\vec F_{2-1} =- \vec F_{1-2}. Como SS es un sistema aislado, podemos asegurar que las fuerzas F⃗2−1,F⃗1−2\vec F_{2-1}, \vec F_{1-2} son las únicas que actúan sobre los sistemas S1,S2S_1, S_2, pudiendo decir que dp⃗1dt=F⃗2−1\frac{d\vec p_1}{dt}= \vec F_{2-1} y que dp⃗2dt=F⃗1−2\frac{d\vec p_2}{dt}= \vec F_{1-2}.

Con todo lo mencionado, podemos afirmar que dp⃗1dt=−dp⃗2dt\frac{d\vec p_1}{dt}= -\frac{d\vec p_2}{dt}. Esto último nos demuestra que en sistemas donde existen al menos dos sub sistemas, la variación de movimiento de uno de ellos, se ve compensado por su contra parte, por lo que la variación total del sistema es siempre nula.

dp⃗1dt+dp⃗2dt=0d(p⃗1+p⃗2)dt=0p⃗1+p⃗2=p⃗S\begin{split} \frac{d\vec p_1}{dt} +\frac{d\vec p_2}{dt} &= 0\\ \frac{d(\vec p_1 + \vec p_2)}{dt} &= 0\\ \vec p_1 + \vec p_2 &= \vec p_S \end{split}

Donde p⃗S\vec p_S es la cantidad de movimiento total del sistema constante. Que dp⃗Sdt=0\frac{d\vec p_S}{dt} = 0 , solo reafirma nuestra hipótesis de que el sistema SS se encuentra aislado, ósea que

dp⃗Sdt=0  ⟺  ∑F⃗externas=0\frac{d\vec p_S}{dt} = 0 \iff \sum \vec F_{\text{externas}} = 0

En un sistema aislado con múltiples partículas interactuando, la suma de las cantidades de movimiento van a ser tal que se anulen entre si mismas, lo que su vez implica que las fuerzas, ahora definidas como fuerzas internas, no pueden formar parte de un análisis físico del sistema, porque se anulan. Las únicas fuerzas que importan son las externas.

Ahora la segunda ley de la conservación resulta ser más relevante ya que se puede aplicar a cualquier sistema de partículas.

p⃗S=cte  ⟺  ∑F⃗externas=0\vec p_S = \text{cte} \iff \sum \vec F_{\text{externas}} = 0

Para expresar adecuadamente que en sistemas donde existen al menos dos sub sistemas, la variación de movimiento de uno de ellos, se ve compensado por su contra parte, por lo que la variación total del sistema es siempre nula, es necesario realizar la siguiente operación.

dp⃗1dt=−dp⃗2dt∫0Δtdp⃗1dt=−∫0Δtdp⃗2dtΔp⃗1=−Δp⃗2Δ(p⃗1+p⃗2)=0\begin{split} \frac{d\vec p_1}{dt} &= -\frac{d\vec p_2}{dt}\\ \int\limits_0^{\Delta t} \frac{d\vec p_1}{dt} &= - \int\limits_0^{\Delta t} \frac{d\vec p_2}{dt}\\ \Delta \vec p_1 &= - \Delta \vec p_2\\ \Delta (\vec p_1 + \vec p_2) &= 0 \end{split}

Ejemplo practico

Supongamos un sistema formado por un arma y una bala. Inicialmente, ambos cuerpos se encuentran en reposo por lo que su cantidad de movimiento es nula. En un instante posterior, la bala fue disparada con una velocidad dada. Lo que se quiere determinar es la velocidad de rebote que percibe la persona que sostiene el arma.

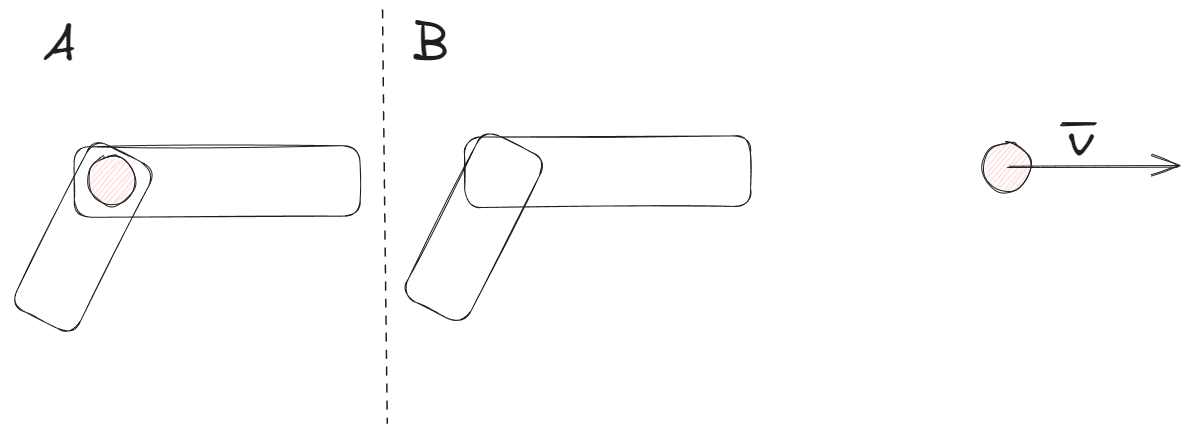
Untitled

En el instante BB, el sistema aun se encuentra aislado, por lo que se puede afirmar que la variación en la cantidad de movimiento del sistema es igual a cero.

Δp⃗arma=−Δp⃗bala\begin{split} \Delta \vec p_{arma} &= - \Delta \vec p_{bala}\\ \end{split}

Como inicialmente tanto la bala como el arma se encontraban en reposo, la variación en la cantidad de movimiento solo esta dada por el estado de ambos subsistemas en el instante BB.

marmavarma=−mbalavbalavarma=−mbalamarmavbala\begin{split} m_{arma}v_{arma} &= - m_{bala}v_{bala}\\ v_{arma} &= -\frac{m_{bala}}{m_{arma}}v_{bala} \end{split}

Como la masa de la bala es significativamente menor que la masa del arma, la relación mbalamarma\frac{m_{bala}}{m_{arma}} hace que la varma≪vbalav_{arma} \ll v_{bala}. De aquí que podemos decir que la velocidad de rebote percibida por el usuario del arma es mínima.

Sistema de partículas

En un sistema SS constituido por nn partículas, podemos decir que

p⃗s=∑i=1np⃗i=∑i=1nmiv⃗i\vec p_s = \sum\limits_{i=1}^n \vec p_i = \sum\limits_{i=1}^n m_i\vec v_i

La variación en la cantidad de movimiento del sistema se puede reflejar en

dp⃗dt=∑i=1ndp⃗idt=∑i=1nF⃗i\frac{d\vec p}{dt} = \sum\limits_{i=1}^n \frac{d\vec p_i}{dt} = \sum\limits_{i=1}^n \vec F_i

Siendo F⃗i\vec F_i la resultante de las fuerzas actuantes sobre la partícula ii. Si resulta que esas fuerzas son solo internas, entonces la cantidad de movimiento del sistema se conserva derivando en resultados ya vistos. En el caso en que existan fuerzas externas, entonces

dp⃗dt=∑i=1nF⃗externas−i\frac{d\vec p}{dt} = \sum\limits_{i=1}^n \vec F_{externas-i}

Es importante entonces que sobre cada partícula actúan tanto fuerzas internas como externas al sistema. Dado que las internas se cancelan entre si, solo restan las externas.

Centro de masa de un sistema de partículas

En un sistema SS constituido por nn partículas, su masa total es igual a la suma de las masas de todas las partículas que la conforman, es decir

M=∑i=1nmiM=\sum\limits_{i=1}^n m_i

La cantidad de movimiento del sistema en su conjunto esta dada por p⃗s=∑i=1nmiv⃗i\vec p_s = \sum\limits_{i=1}^n m_i\vec v_i y por p⃗s=MVcm\vec p_s = MV_{cm}, donde VcmV_{cm} es la velocidad del centro de masa. Dicho esto, es fácil ver que

V⃗cm=∑i=1nmiv⃗iM\vec V_{cm} = \frac{\sum\limits_{i=1}^n m_i\vec v_i}{M}

Esto quiere decir que la velocidad del centro de masa es un promedio ponderado de las velocidades de las partículas que la conforman, en relación al aporte de su masa a la masa total.

Dado que v⃗i=r⃗i˙\vec v_i = \dot{\vec r_i}, es posible integrar la expresión anterior y conseguir finalmente la posición del centro de masa.

R⃗cm=∑i=1nmir⃗iM\vec R_{cm} = \frac{\sum\limits_{i=1}^n m_i\vec r_i}{M}

Suena trivial decirlo, pero vale la pena mencionarlo. La posición del centro de masa es un promedio ponderado de las posiciones de las partículas que la conforman, en relación al aporte de su masa a la masa total.

No son triviales ambas menciones, tanto con VcmV_{cm}, como con RcmR_{cm}, ya que intuitivamente podemos dar ciertas afirmaciones en determinados problemas con solo ver las masas que conforman un sistema.

Lo interesante de los resultados vistos hasta el momento radica principalmente en el hecho de que podemos dejar la joven idea de hablar sobre objetos puntuales con una velocidad y una posición dada, para madurar a un pensamiento mucho más realista donde los objetos pueden ser mucho más complejos y aun así, pueden ser descriptos con facilidad.

De la expresión p⃗s=MVcm\vec p_s = MV_{cm}, aplicando derivada se puede ver la siguiente expresión un tanto conocida

∑F⃗ext=MA⃗cm\sum \vec F_{ext} = M\vec A_{cm}

Donde AcmA_{cm} es la aceleración del centro de masa. Es de aquí que podemos afirmar que si el conjunto de fuerzas externas aplicada sobre un sistema se anulan entre si, entonces la velocidad del centro de masa resultara constante, dando por consiguiente, un movimiento del tipo rectilíneo uniforme.

Colisiones

Colisiones plásticas

Si bien podemos visualizar y determinar la dinámica de dos cuerpos desde un sistema de referencia fijo externo como lo puede ser el de laboratorio, todo cambia cuando poseemos el concepto de centro de masa, dado que ahora podemos localizar nuestro sistema de referencia fijo en él.

Localizar el sistema de referencia sobre el centro de masa de un sistema tiene algunas ventajas. Supongamos que sobre unos rieles, se encuentran dos vagones. Inicialmente, el vagón b1b_1 posee una velocidad v1v_1, mientras que el vagón b2b_2 se mantiene en reposo

Si tras colisionar, estos se mantienen unidos en lo que se conoce como un choque plástico, debemos determinar cual es la velocidad final del sistema.

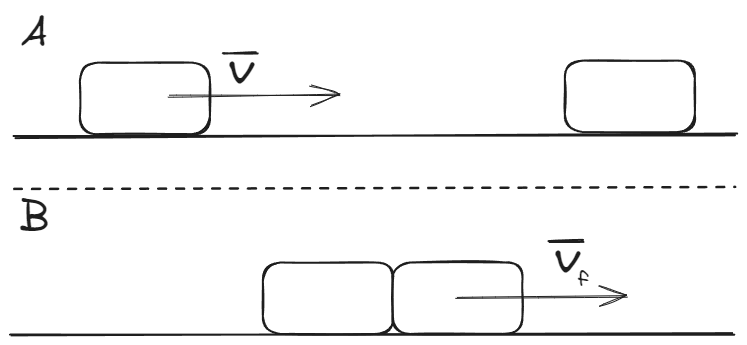
Untitled

Digamos que ambos vagones tienen la misma cantidad de masa mm. Dado que las únicas fuerzas externas son las de peso y la normal, ambas se anulan, conservando la cantidad de movimiento del sistema.

Esto quiere decir que la cantidad de movimiento en el instante AA, debe ser la misma que en el instante BB.

p⃗A=p⃗Bm1v⃗1=(m1+m2)v⃗fmv⃗1=2mv⃗f12v⃗1=v⃗f\begin{split} \vec p_A &= \vec p_B\\ m_1\vec v_1 &= (m_1 + m_2)\vec v_f\\ m\vec v_1 &= 2m\vec v_f\\ \frac{1}{2}\vec v_1 &=\vec v_f \end{split}

Si pretendemos resolver la misma situación desde un sistema de referencia puesto sobre el centro de masa del sistema, deberemos usar un tipo de análisis relativo donde

v⃗1−cm=v⃗1−v⃗cmv⃗2−cm=v⃗2−v⃗cm\begin{split} \vec v_{1-cm} &= \vec v_1 - \vec v_{cm}\\ \vec v_{2-cm} &= \vec v_2 - \vec v_{cm}\\ \end{split}

Por lo que sabemos, la velocidad del centro de masa se puede calcular como

V⃗cm=∑i=1nmiv⃗iMV⃗cm=mv⃗12mV⃗cm=v⃗12\begin{split} \vec V_{cm} &= \frac{\sum\limits_{i=1}^n m_i\vec v_i}{M}\\ \vec V_{cm} &= \frac{m\vec v_1}{2m}\\ \vec V_{cm} &= \frac{\vec v_1}{2}\\ \end{split}

Dicho esto, podemos calcular la velocidad de cada uno de los vagones con respecto al centro de masa.

v⃗1−cm=v⃗1−12v⃗1=12v⃗1v⃗2−cm=v⃗2−v⃗cm=−12v⃗1\begin{split} \vec v_{1-cm} &= \vec v_1 - \frac{1}{2}\vec v_1 = \frac{1}{2}\vec v_1\\ \vec v_{2-cm} &= \vec v_2 - \vec v_{cm}=-\frac{1}{2}\vec v_1\\ \end{split}

Este resultado nos indica que desde la perspectiva del centro de masa, ambos vagones se acercan a igual velocidad. Cuando finalmente se encuentran y quedan “pegadas” por así decirlo, lo hacen en el punto cero y se quedan juntas, por lo que la velocidad final es cero, esto visto desde el centro de masa.

p⃗A=p⃗Bm12v⃗1−m12v⃗1=p⃗B0=p⃗B\begin{split} \vec p_A &= \vec p_B\\ m\frac{1}{2}\vec v_1 - m\frac{1}{2}\vec v_1 &= \vec p_B\\ 0 &= \vec p_B\\ \end{split}

Colisiones elásticas e inelásticas

En lo que a colisiones se refiere, existen dos variables. Por un lado la cantidad de movimiento, que en general es constante y por el otro, la energía. En el caso de las explosiones o los choque plásticos, la energía no se conserva. En el primer caso, hay un incremento de energía expresado en la velocidad, mientras que el segundo caso, hay un decremento de energía que se pierde en la deformación de los cuerpos.

En los choques elásticos, la energía cinética si se conserva. Esto característica es la diferencia que posee con las colisiones inelásticas, donde la cantidad de movimiento se conserva, pero la energía se disipa en la deformación de alguno de los cuerpos.

Para poner en practica y entender mejor los conceptos mencionados, veamos un ejemplo clave. Sea un sistema de dos partículas con masas m1,m2m_1, m_2 y velocidades iniciales v1,v2v_1, v_2 respectivamente.

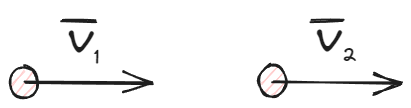
Untitled

Se desea conocer las velocidades adquiridas por cada uno de las partículas tras un choque del tipo elástico. De acuerdo a los datos, se pueden expresar las siguientes ecuaciones del estado inicial del sistema

p0=m1v1+m2v2p_0 = m_1v_1 + m_2v_2
Ec0=12m1v12+12m2v22E_{c0} = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2

En un estado post colisión nos encontramos con las siguientes ecuaciones e incógnitas

pf=m1v1f+m2v2fp_f = m_1v_{1f} + m_2v_{2f}
Ecf=12m1v1f2+12m2v2f2E_{cf} = \frac{1}{2}m_1v_{1f}^2 + \frac{1}{2}m_2v_{2f}^2

Por la conservación en la cantidad de movimiento y energía, se plantean las siguientes equivalencias.

p0=pfm1v1+m2v2=m1v1f+m2v2fm1(v1f−v1)=m2(v2f−v2)\begin{split} p_0 &= p_f\\ m_1v_1 + m_2v_2 &= m_1v_{1f} + m_2v_{2f}\\ m_1(v_{1f} - v_1) &= m_2(v_{2f} - v_2) \end{split}
Ec0=Ecf12m1v12+12m2v22=12m1v1f2+12m2v2f2m1(v1f2−v12)=m2(v2f2−v22)\begin{split} E_{c0} &= E_{cf} \\ \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 &= \frac{1}{2}m_1v_{1f}^2 + \frac{1}{2}m_2v_{2f}^2 \\ m_1(v_{1f}^2 - v_1^2) &= m_2(v_{2f}^2 - v_2^2)\\ \end{split}

Por la propiedad A2−B2=(A−B)(A+B)A^2 - B^2 = (A-B)(A+B), podemos expresar la segunda ecuación como

m1(v1f−v1)(v1f+v1)=m2(v2f−v2)(v2f+v2)m_1(v_{1f} - v_1)(v_{1f} + v_1) = m_2(v_{2f} - v_2)(v_{2f} + v_2)

Y si se realiza un cociente entre la expresión recién mostrada y la primera ecuación, llegamos a la siguiente igualdad

(v1f+v1)=(v2f+v2)(v_{1f} + v_1) = (v_{2f} + v_2)

De esta última ecuación y la primera se pueden despejar las incógnitas v1f,v2fv_{1f},v_{2f} y responder a la pregunta inicial.

v1f=m1−m2m1+m2v1+2m2m1+m2v2v_1f = \frac{m_1 - m_2}{m_1 + m_2}v_1 + \frac{2m_2}{m_1 + m_2}v_2
v2f=m2−m1m1+m2v2+2m1m1+m2v1v_2f = \frac{m_2 - m_1}{m_1 + m_2}v_2 + \frac{2m_1}{m_1 + m_2}v_1

De estas expresiones podemos verificar que ocurre en ciertos casos borde donde la velocidad inicial de alguno de los cuerpo es cero o que un cuerpo es significativamente más masivo que el otro.

Características adicionales del centro de masa

  1. Si un sistema esta formado por dos partículas, entonces el centro de masa del sistema se encuentran entre ambas partículas y sobre la recta que las une.
  2. En sistemas de partículas homogéneas o simétricas, el centro de masa puede ser calculado de forma geométrica. Por ejemplo, el centro de masa de una esfera homogénea (no existe un sector más denso que otro), el centro de masa será el centro de la esfera. Esto puede tomarse como generalización del punto anterior, para el caso en que ambas partículas tienen la misma masa.
  3. Sea un sistema conformado por cuerpos homogéneos, se puede calcular el centro de masa del sistema a partir del centro de masa de cada uno de los cuerpos. Esto también se puede entender como una generalización del punto uno, donde las partículas representan el centro de masa de los cuerpo.