profile photo

Guía 5 - Impulso angular


hero image
Publicado el

Impulso angular

El concepto de impulso angular es análogo a de impulso lineal (cantidad de movimiento), pero que adquiere relevancia cuando el movimiento a describir no es rectilíneo.

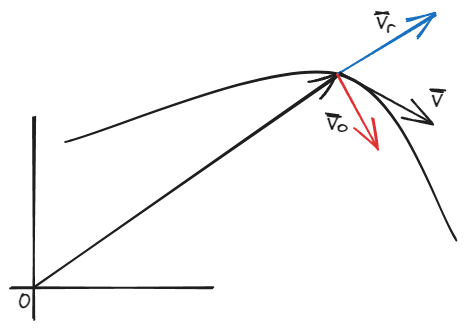
Untitled

Uno siempre puede describir un movimiento como una combinación de dos movimientos, uno radial (vrv_r) y otro angular (vθv_\theta). Desde esta perspectiva, la cantidad de movimiento se puede expresar como

p⃗=mv⃗θ+mv⃗r\vec p = m\vec v_\theta + m\vec v_r

Dicho lo anterior, podemos definir al impulso angular como

L⃗0=r⃗×p⃗=r⃗×(mv⃗θ+mv⃗r)=r⃗×mv⃗θ+r⃗×mv⃗r=r⃗×mv⃗θ\begin{split} \vec L_0 &= \vec r \times \vec p\\ &= \vec r \times (m\vec v_\theta + m\vec v_r)\\ &= \vec r \times m\vec v_\theta + \vec r \times m\vec v_r \\ &= \vec r \times m\vec v_\theta \end{split}

Observamos entonces que el impulso angular como un producto vectorial entre el vector de posición y la velocidad angular, que da como resultado un vector perpendicular al plano formado por los vectores r⃗,v⃗θ\vec r, \vec v_\theta, y que es máximo dado que dichos vectores son perpendiculares a su vez. De aquí que al impulso angular también se lo conoce como momento de la componente angular del impulso o momento angular para abreviar.

Notemos que L⃗\vec L depende directamente del sistema de referencia o desde donde se lo observe. A este punto desde el cual se define al momento se lo conoce como centro de momentos.

Es entonces que podemos relativizar a L⃗\vec L si lo observamos desde otro punto de referencia.

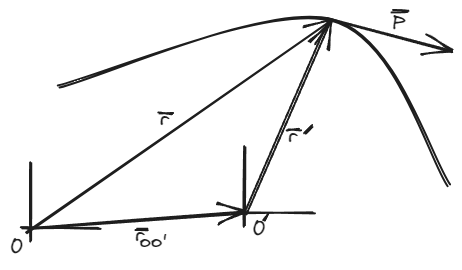
Untitled

Es así que podemos observar como cambia L⃗\vec L visto desde otro punto O′O^\prime.

L⃗o=r⃗×p⃗=(r⃗′+r⃗oo′)×p⃗=r⃗′×p⃗+roo′×p⃗=L⃗o′+roo′×p⃗\begin{split} \vec L_o &= \vec r \times \vec p\\ &= (\vec r^\prime + \vec r_{oo^\prime}) \times \vec p\\ &= \vec r^\prime \times \vec p + r_{oo^\prime} \times \vec p\\ &= \vec L_{o^\prime} + r_{oo^\prime} \times \vec p \end{split}

Tanto OO como O′O^\prime pueden ser puntos cualquiera de un mismo sistema de referencia. No tienen porque ser el origen de un sistema de coordenadas.

Ley de conservación del impulso angular

Así como p⃗\vec p, L⃗\vec L también puede permanecer constante dadas ciertas condiciones. Si entendemos a L⃗o=r⃗×p⃗\vec L_o = \vec r \times \vec p, entonces su derivada se expresa como

L⃗o˙=r⃗˙×p⃗+r⃗×p⃗˙=v⃗×p⃗+r⃗×F⃗=r⃗×F⃗\begin{split} \dot{\vec L_o} &= \dot{\vec r} \times \vec p + \vec r \times \dot{\vec p}\\ &= \vec v \times \vec p + \vec r \times \vec F\\ &= \vec r \times \vec F \end{split}

A esta última expresión se la conoce como momento de fuerza externas o torque, y se lo simboliza como M⃗oext\vec M_o^{ext}. Entonces, para que L⃗\vec L sea constante es importante que su derivada valga cero, es decir, M⃗oext=0\vec M_o^{ext} = 0, y esto es si y solo si, la resultante de las fuerzas externas y el vector de posición son paralelos. En ese caso, definimos a las fuerzas existentes como centrales.

Es interesante observar que si el impulso lineal se conserva, tenemos un movimiento rectilíneo uniforme. Si el impulso angular se conserva, entonces tenemos un movimiento circular uniforme, esto visto desde el centro de momentos.

Por otro lado, si el movimiento que describe un cuerpo es rectilíneo, siempre podremos encontrar un centro de momentos tal que el impulso angular se conserve.

Centro de momentos móvil

Anteriormente dimos a conocer los conceptos validos para calcular L⃗\vec L desde centro de momentos alternativos, llegando a la expresión

L⃗o=L⃗o′+roo′×p⃗\vec L_o= \vec L_{o^\prime} + r_{oo^\prime} \times \vec p

Supongamos ahora que el centro de momentos alternativo o′o^\prime se encuentra en movimiento con una velocidad v⃗oo′\vec v_{oo^\prime}. El cambio en relación al impulso angular L⃗o′\vec L_{o^\prime}, se puede resumir en

L⃗o′=L⃗o−r⃗oo′×p⃗L⃗o′˙=L⃗o˙−(r⃗oo′˙×p⃗+r⃗oo′×p⃗˙)M⃗o′ext=M⃗oext−v⃗oo′×p⃗−r⃗oo′×p⃗˙\begin{split} \vec L_{o^\prime} &= \vec L_o - \vec r_{oo^\prime} \times \vec p\\ \dot{\vec L_{o^\prime}} &= \dot{\vec L_o} -( \dot{\vec r_{oo^\prime}} \times \vec p + \vec r_{oo^\prime} \times \dot{\vec p})\\ \vec M_{o^\prime}^{ext}&= \vec M_o^{ext} - \vec v_{oo^\prime} \times \vec p - \vec r_{oo^\prime} \times \dot{\vec p}\\ \end{split}

Primer ejemplo practico

Sea un cuerpo de masa mm con una velocidad constante v⃗\vec v, que gira en torno a un centro de rotación (crcr), a una distancia RR. Se desea calcular el impulso angular que adquiere el cuerpo visto desde un punto oo que se encuentra en el mismo eje que el centro de rotación pero a una distancia desconocida.

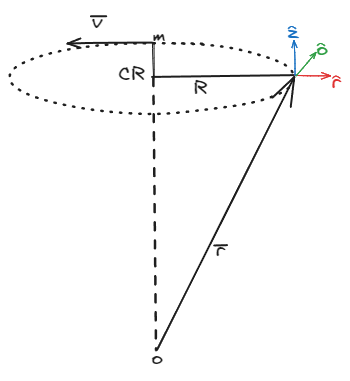
Untitled

Los datos serán expresados en torno a los versores r^,θ^,z^\hat r, \hat \theta, \hat z. Dicho todo lo anterior, podemos decir que el impulso angular del cuerpo puede expresarse como

L⃗o=r⃗×p⃗=(Rr^+zz^)×(mωRθ^)=Rr^×mωRθ^+zz^×mωRθ^=∣R∣∣mωR∣z^−∣z∣∣mωR∣r^=mωR2z^−zmωRr^\begin{split} \vec L_o &= \vec r \times \vec p\\ &= (R\hat r + z\hat z) \times (m\omega R \hat\theta)\\ &= R\hat r \times m\omega R \hat\theta + z\hat z \times m\omega R \hat\theta\\ &=|R||m\omega R|\hat z - |z||m\omega R|\hat r \\ &= m\omega R^2 \hat z - zm\omega R \hat r \end{split}

Rápidamente observamos que por tener una componente en el versor r^\hat r, el impulso angular cambia, lo que implica que el momento de fuerzas externas es distinto de cero, lo que a su vez, indica que existen fuerzas no centrales. Estos resultados a priori no coinciden con un movimiento circular y uniforme.

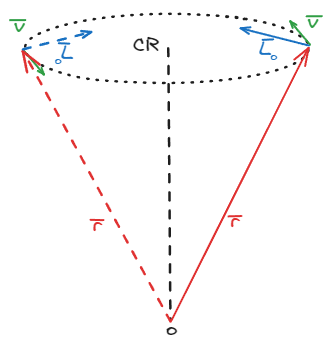
Untitled

Si bien es cierto que L⃗o\vec L_o cambia dada su componente en r^,\hat r, no es así con su componente en z^\hat z, lo que nos indica que el cuerpo se esta moviendo en un plano que por el momento desconocemos.

Si cambiamos las condiciones del problema y observamos el impulso angular desde el centro de rotación, la componente en r^\hat r de los resultados iniciales se anula automáticamente, dado que z=0z = 0 . En su lugar, L⃗o\vec L_o queda representado únicamente por su componente en z^\hat z, que como ya dijimos, es constante, lo que implica que el torque es nulo. Esto último confirma que el movimiento presentado por el cuerpo es del tipo circular y uniforme, plantado sobre el plano perpendicular al versor z^\hat z.

Lo que destacamos de las recientes conclusiones es que el impulso angular no solo nos puede ayudar a conocer la dinámica del cuerpo, sino que además, puede dar pistas sobre la trayectoria que sigue el objeto en estudio.

Segundo ejemplo practico

Supongamos un cuerpo de masa mm que se mueve a una velocidad constante en línea recta. Se desea conocer el impulso angular del objeto visto desde el punto oo.

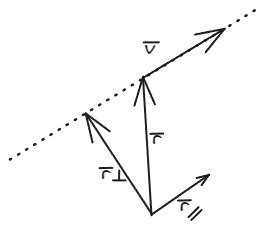
Untitled

El vector de posición puede ser visto como una composición de dos vectores, uno que es paralelo a la trayectoria del cuerpo, y otro que es perpendicular. Llamemos r⃗t\vec r_t a la proyección perpendicular y r⃗l\vec r_l al paralelo.

Entonces, procedemos a calcular el impulso angular del cuerpo

L⃗o=r⃗×mv⃗=(r⃗t+r⃗l)×mv⃗=r⃗t×mv⃗+r⃗l×mv⃗=r⃗t×mv⃗\begin{split} \vec L_o &= \vec r \times m\vec v\\ &= (\vec r_t + \vec r_l) \times m\vec v\\ &= \vec r_t\times m\vec v + \vec r_l\times m\vec v\\ &= \vec r_t\times m\vec v \end{split}

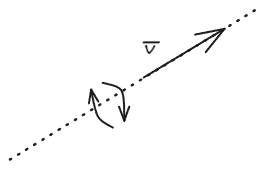
La componente r⃗t\vec r_t tiene la particularidad de que es constante, por lo que el impulso angular es constate. En este caso, el movimiento descripto por el cuerpo no es un movimiento circular uniforme, pero aún así, muestra un impulso angular constante.

En el caso del impulso lineal, uno decía que si este es constante, entonces necesariamente existe un movimiento rectilíneo uniforme, pero en el caso del impulso angular, que este último sea constate, puede significar que estemos frente a un MCUMCU o MRUMRU, y que es ambos tienen una dinámica simétrica.

En el MCU, el movimiento es simétrico respecto al centro de rotación donde debe estar contenido el centro de momentos. En MRUMRU, es simétrico en su rotación en torno a su trayectoria (que es nula, pero eso también es simetría).

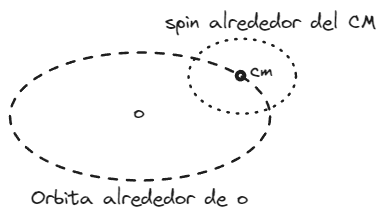
Untitled

Impulso angular en un sistema de partículas

Podemos decir que el impulso angular de un sistema de partículas visto desde un punto oo es

L⃗o=∑i=1nL⃗i=∑i=1nr⃗i×p⃗i\begin{split} \vec L_o &= \sum\limits_{i=1}^n \vec L_i\\ &= \sum\limits_{i=1}^n \vec r_i \times \vec p_i \end{split}

Ahora realizaremos una reinterpretación importante para la resolución del problema. Al vector de posición de cada partícula se lo representa de la siguiente forma

r⃗i=r⃗i−R⃗cm+R⃗cm=(r⃗i−R⃗cm)+R⃗cm=r⃗i′+R⃗cm\begin{split} \vec r_i &= \vec r_i - \vec R_{cm} + \vec R_{cm}\\ &= (\vec r_i - \vec R_{cm}) + \vec R_{cm}\\ &= \vec r_i^\prime + \vec R_{cm}\\ \end{split}

Donde R⃗cm\vec R_{cm} es la posición del centro de masa del sistema y r⃗i′\vec r_i^\prime es la posición de la partícula ii visto desde el centro de masa. Aplicando esta nueva expresión a L⃗o\vec L_o se obtiene

L⃗o=∑i=1nL⃗i=∑i=1nr⃗i×p⃗i=∑i=1n(r⃗i′+R⃗cm)×p⃗i=∑i=1nr⃗i′×p⃗i+R⃗cm×p⃗i=∑i=1nr⃗i′×p⃗i+∑i=1nR⃗cm×p⃗i=∑i=1nr⃗i′×p⃗i+R⃗cm×∑i=1np⃗iL⃗o=L⃗cm+R⃗cm×P⃗\begin{split} \vec L_o &= \sum\limits_{i=1}^n \vec L_i\\ &= \sum\limits_{i=1}^n \vec r_i \times \vec p_i\\ &= \sum\limits_{i=1}^n (\vec r_i^\prime + \vec R_{cm}) \times \vec p_i\\ &= \sum\limits_{i=1}^n \vec r_i^\prime\times \vec p_i + \vec R_{cm}\times \vec p_i \\ &= \sum\limits_{i=1}^n \vec r_i^\prime\times \vec p_i + \sum\limits_{i=1}^n\vec R_{cm}\times \vec p_i \\ &= \sum\limits_{i=1}^n \vec r_i^\prime\times \vec p_i + \vec R_{cm}\times\sum\limits_{i=1}^n \vec p_i \\ \vec L_o &= \vec L_{cm} +\vec R_{cm} \times \vec P \end{split}

Es decir que el impulso angular de un sistema de partículas queda descripto a partir del impulso angular visto desde el centro de masa y por el impulso angular de un “todo” contenido en una partícula localizado en la posición del centro de masa. El componente L⃗cm\vec L_{cm} se lo conoce como impulso angular de spin que nos permita ver al sistema desde el centro de masa. Mientras que al componente R⃗cm×P⃗\vec R_{cm} \times \vec P se lo conoce como impulso angular orbital que nos permite ver al sistema como un todo desde el punto oo.

Untitled