Guía 4 - Trabajo y energía

Publicado el 5/8/2023

Trabajo

De forma muy coloquial, podemos definir al trabajo como la cantidad de energía necesaria para mover un objeto a través de una distancia dada mediante una fuerza sostenida. El trabajo se mide en Joules (J) y en general, se lo denota con la letra $W$ o $L$ .

Untitled

Por experiencia, sabemos que cuanto más larga sea la distancia a recorrer, mayor será el esfuerzo requerido, es decir, $W \propto |\Delta x|$ .

Supongamos ahora que para la misma distancia, se aplican dos magnitudes de fuerza $\vec F_1, \vec F_2$ distintas, donde $|\vec F_1| < |\vec F_2|$ . Es claro que las cantidades de energía utilizadas en cada caso no será la misma. Concretamente, se requerirá de más trabajo cuanto más fuerza sea utilizada, o sea, $W \propto |\vec F|$ .

Pareciera que tenemos todas las magnitudes requeridas para el concepto de trabajo, pero es importante mencionar dos salvedades.

Las trayectorias no necesariamente son rectilíneas.
La fuerza o resultante de fuerza no están obligadas a ser colineales al desplazamiento

Como el camino a realizar no necesariamente es rectilíneo, debemos ver al desplazamiento como un vector diferencial en un punto particular de la trayectoria y tangente a la misma. Lo denotamos con $d\vec r = (dx, dy)$ .

Untitled

A ese diferencial lo podemos multiplicar por la fuerza, para luego componerlos para cada punto de la trayectoria y obtener así, el trabajo requerido para ir del punto $A$ al $B$ .

Untitled

Por otro lado, imaginemos el escenario en que una persona tira de una caja mediante una cuerda para deslizarla por el piso. Es evidente que la fuerza aplicada sobre la caja no esta en la misma dirección que su desplazamiento. Ciertamente nos va interesar la componente de $\vec F$ que si es colineal con el movimiento, pero eso no quita el hecho de que existe un cierto ángulo $\alpha$ que los separa.

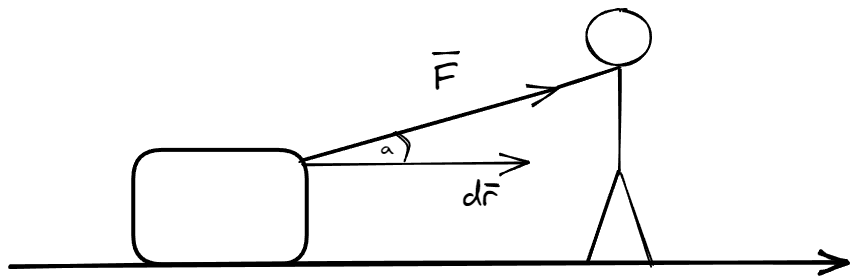
Untitled

Si aplicamos producto escalar entre $\vec F$ y $d\vec r$ , lo que obtenemos es el trabajo para un punto particular de la trayectoria, es decir

dW = \vec F \cdot d\vec r= |\vec F||d\vec r|\cos \alpha

Si integramos esta expresión para dos puntos $A,B$ , llegamos finalmente a la expresión de trabajo.

\begin{split} W &= \int_A^B\vec F \cdot d\vec r \end{split}

La expresión depende del sistema de coordenadas. Por ejemplo, en el sistema cartesiano, el trabajo se puede expresar como

W= \int_{A_x}^{B_x} F_x d_x + \int_{A_y}^{B_y} F_y d_y

Corolarios

Anteriormente dijimos que de la fuerza aplicada sobre un objeto, nos va a interesar su componente en dirección al desplazamiento, ya que esta es la que finalmente genera trabajo. Pues bien, resulta que

\begin{split} dW &= |\vec F||d\vec r|\cos \alpha \\ &= |\vec F|\cos \alpha |d\vec r|\\ &= F_{dr} |d\vec r| \end{split}

Donde $F_{dr}$ es la proyección de $\vec F$ en la dirección de $d\vec r$ , y dependiendo del ángulo $\alpha$ , $dW$ puede ser positivo, negativo o nulo

Si $\alpha < \frac{\pi}{2} \rightarrow \cos \alpha > 0 \rightarrow dW>0$ . Esto estaría indicando que el trabajo es funcional al desplazamiento (lo ayuda o lo genera).
Si $\frac{\pi}{2}<\alpha < \pi \rightarrow \cos \alpha < 0 \rightarrow dW <0$ . En este caso, se esta ejerciendo trabajo para detener un objeto en movimiento.
Si $\alpha = \frac{\pi}{2} \rightarrow \cos \alpha = 0 \rightarrow dW=0$ . La fuerza es perpendicular al desplazamiento, por lo que no puede generar trabajo alguno, lo que no significa que el objeto no se encuentre en movimiento.

Por último, si la fuerza $\vec F$ es constante, entonces el trabajo se puede calcular como:

W = \vec F \cdot \Delta \vec r

En el caso en que la trayectoria sea recta, entonces el trabajo lo podemos calcular como:

W = |\vec F | |\Delta \vec r| \cos(\alpha)

Ejemplo

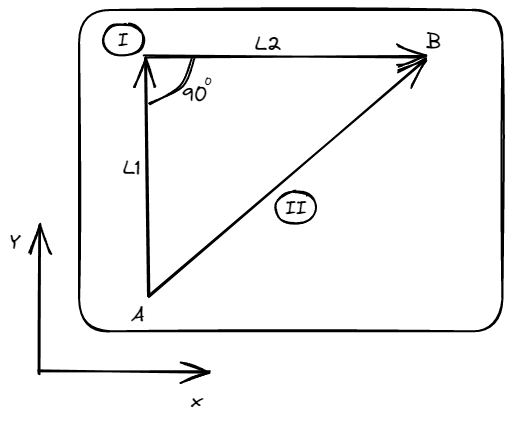
Enunciado: Sea un objeto $m$ que movemos sobre una mesa desde un punto $A$ hasta un punto $B$ a través de dos trayectorias distintas $I, II$ , donde la trayectoria $I$ esta compuesta de dos tramos de longitud $L_1, L_2$ tal que $L_1 =L_2=L$ , a una velocidad constante. Determinar cual es el trabajo realizado por la fuerza encargada de mover el cuerpo sobre la mesa en cada trayectoria teniendo en cuenta que existe rozamiento entre el objeto y la superficie del mueble.

Untitled

Dado que existe rozamiento entre el cuerpo y la mesa, la fuerza necesaria para mover el objeto debe ser igual al rozamiento dinámico presente. No puede ser menor, porque en ese caso, el cuerpo no se movería, y tampoco puede ser mayor, ya que se produciría aceleración.

F - \mu N = 0 \rightarrow F = \mu N

Trabajo en la trayectoria $I$ : Debemos atender al hecho de que cualquiera de las trayectorias observadas en este caso son rectilíneas, por lo que el trabajo se simplifica bastante.

Por un lado en el tramo $L_1$ , $d\vec r = dy \hat y$ , siendo que la fuerza aplicada es $\vec F = -\mu_d N \hat y$ , mientras que en tramo $L_2$ , $d\vec r = dx \hat x$ , y la fuerza empleada es $\vec F = -\mu_d N \hat x$ . Esto se concluye con el trabajo calculado como

\begin{split} W_I &= \int_{L_1}\vec F \cdot d\vec r + \int_{L_2}\vec F \cdot d\vec r\\ &= \int_{y_i}^{y_f}\mu_d N dy + \int_{x_i}^{x_f}\mu_d N dx\\ &= \mu_d N(y_f - y_i) +\mu_d N(x_f - x_i)\\ &= 2\mu_d NL \end{split}

Trabajo en la trayectoria $II$ : Para este caso, es fácil ver que la trayectoria es rectilínea, y por Pitágoras, podemos decir que su longitud equivale a $\sqrt 2 L$ . Sin embargo, si mantenemos el mismo sistema de referencia que en el primer caso, las cuentas se complicarían, y nada nos impide tomar otro sistema de referencia tal como se muestra en el siguiente grafico.

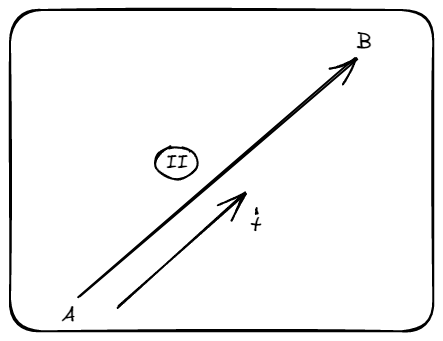
Untitled

Con esto en mente, podemos decir que $d\vec r = dx^\prime \hat x^\prime$ y que $\vec F = -\mu N \hat x^\prime$ , con lo cual, podemos decir que el trabajo empleado para esta trayectoria es

\begin{split} W_{II} &= \int_{\vec {r_{i}}}^{\vec {r_{f}}} \vec F \cdot d\vec r\\ &= \mu_d N \int_{x_{i}^{\prime}}^{x_{f}^{\prime}}dx^\prime\\ &=\mu_d N (x_{f}^{\prime}-x_{i}^{\prime})\\ &= \mu_d N \sqrt 2 L \end{split}

Lo que concluimos es que $W_I > W_{II}$ , por lo que podemos empezar a intuir que el trabajo depende de la trayectoria realizada, pero se advierte que no siempre es así y ahora veremos un ejemplo de ello.

Fuerzas conservativas

Llamamos fuerzas conservativas a aquellas que tienen la propiedad de que el trabajo que realizan es independiente de la trayectoria seguida y solamente depende de los puntos inicial y final. Algunos ejemplos de fuerzas conservativas son la fuerza gravitatoria y la fuerza elástica.

Veamos un ejemplo. Supongamos ahora que deseamos mover una carga a una velocidad constante desde un punto $A$ hasta un punto $B$ con un montacargas. Los tramos $L_1, L_2$ son iguales y por tanto lo podemos definir como de longitud $L$ .

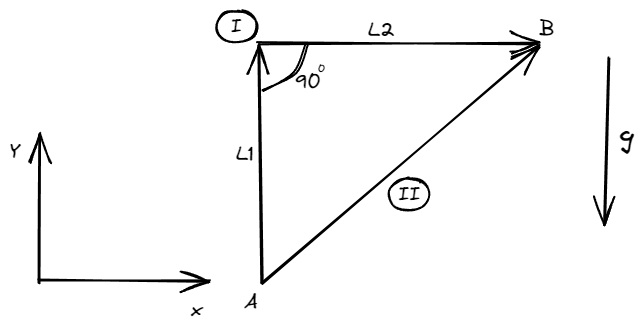
Untitled

Al igual que antes tenemos dos trayectorias posibles. La fuerza encargada de realizar trabajo en este caso es la que debe elevar a la carga por encima del suelo y debe ser igual al peso a sostener, es decir que $\vec F = mg \hat y$ .

Para la primera trayectoria decimos que:

\begin{split} W_I &= \int_{L_1}\vec F \cdot d\vec r + \int_{L_2}\vec F \cdot d\vec r\\ &= \int_{L_1} mg\hat y \cdot dy \hat y + \int_{L_2} mg\hat y \cdot dx \hat x\\ &= \int_{L_1} mg\hat y \cdot dy \hat y\\ &= \int_{L_1} mg\space dy\\ &= mgL \end{split}

Observar como el trabajo en el segundo tramo de la trayectoria se cancela debido a que la fuerza es perpendicular a la trayectoria.

Calculemos lo que ocurre en la segunda trayectoria, adoptando un nuevo sistema de referencia:

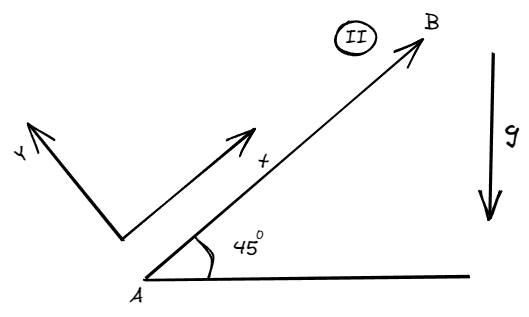
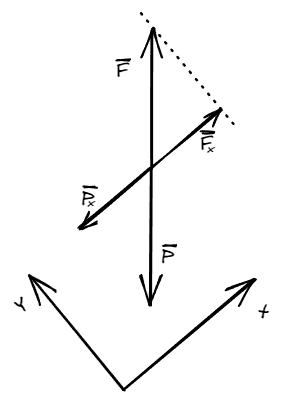
Untitled

En esta nuevas condiciones, la fuerza encargada de dar movimiento a la carga es $\vec F_{x^\prime} = \sin(\frac{\pi}{4}) mg \hat x^\prime = \frac{1}{\sqrt 2} mg\hat x^\prime$ . Por tanto el trabajo a realizar es:

\begin{split} W_{II} &= \int_{\vec {r_{i}}}^{\vec {r_{f}}} \vec F_{x^\prime} \cdot d\vec r\\ &= \frac{1}{\sqrt 2} mg \int_{x_{i}^{\prime}}^{x_{f}^{\prime}}dx^\prime\\ &= \frac{1}{\sqrt 2} mg \sqrt 2 L\\ &= mgL \end{split}

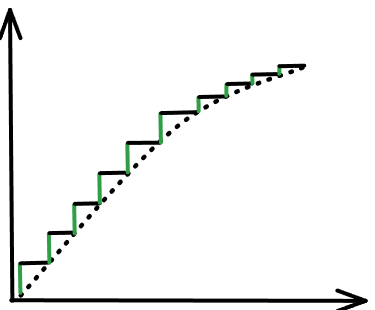
El trabajo realizado es el mismo en ambas trayectorias. ¿Podemos decir entonces que el peso es una fuerza conservativa?. Lamentablemente un caso no hace a la generalidad. Pero pensemos de la siguiente forma: cualquier trayectoria puede ser aproximada mediante “escaleras” continuas. Dado esto, es fácil ver como el peso solo realizara trabajo en los movimientos verticales, dando por resultado que lo único importe es la altura, y no la trayectoria. Ahora si, podemos afirmar que el peso es una fuerza conservativa ya que su trabajo, es independiente de la trayectoria.

Untitled

Corolarios

En un camino cuya longitud es distinta de cero que termina en el mismo punto por donde empieza, o sea, un camino cerrado, el trabajo de una fuerza conservativa siempre será igual a cero y se lo expresa de la siguiente forma:

\oint\vec F \cdot d\vec r = 0 \iff \vec F \text{ es conservativa}

Por otro lado, las fuerzas conservativas solo dependen de la posición, de nada más.

Energía

En física, se define la energía como la capacidad de un sistema para realizar trabajo. Esta capacidad de realizar trabajo se debe a la presencia de una fuerza que actúa sobre el objeto en cuestión. La energía se mide en Joules (J) y se denota con la letra $E$ .

La energía es una cantidad escalar que puede existir en diferentes formas. Algunas formas de energía incluyen la energía cinética, la energía potencial, la energía térmica, entre otras.

Energía Cinética

Supongamos por un momento que se aplica una fuerza $\vec F$ constante sobre un cuerpo para trasladarlo desde una posición $x_i$ hasta $x_f$ . A la vez, el cuerpo parte una velocidad $v_i$ y llega al punto final con una velocidad $v_f$ , es decir, existe aceleración.

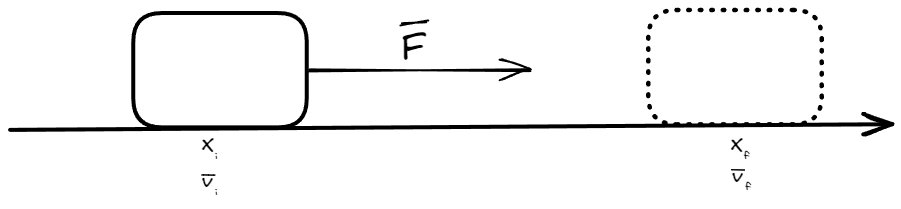
Untitled

Dadas las condiciones, podemos expresar el trabajo realizado por la fuerza como:

W = F\Delta x

Usando la segundo ley de Newton, podemos expresar el trabajo como:

W=ma\Delta x

Esto en vistas de que la fuerza es colineal con el desplazamiento y que la trayectoria es en línea recta, lo que se traduce inmediatamente en un movimiento rectilíneo uniformemente variado, por lo que se puede expresar la velocidad del cuerpo en función de la posición.

v_f^2 = v_i^2 + 2a\Delta x

Esta expresión la podemos cambiar por

a\Delta x = \frac{v_f^2 - v_i^2}{2}

Reformulando la definición de trabajo como

\begin{split} W &= m\frac{v_f^2 - v_i^2}{2}\\ &= \frac{mv_f^2}{2} - \frac{mv_i^2}{2} \end{split}

La energía cinética la podemos definir como $E_c = \frac{1}{2}mv^2$ . Es una forma de energía asociada al movimiento de un objeto, y su magnitud depende tanto de la masa del objeto como de su velocidad. Cualquier objeto que se mueve tiene energía cinética, y esta energía puede ser transferida a otros objetos al colisionar con ellos o al realizar trabajo sobre ellos.

Dicho esto, podemos ver que el trabajo de un cuerpo en MRUV, lo podemos definir como la variación de energía cinética:

W = E_{cf} - E_{ci} = \Delta E_c

En este punto, la relación entre trabajo y energía se hace evidente, aclarando las definiciones dadas hasta el momento.

Un caso ejemplar del movimiento cinético es el del movimiento circular uniforme, donde la velocidad tangencial es constante y la única fuerza presente es la centrípeta.

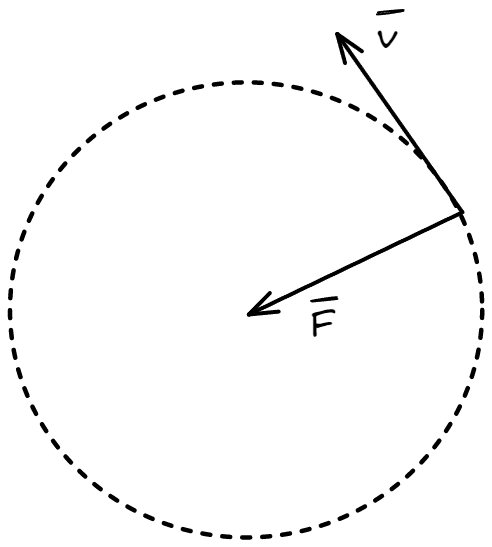
Untitled

Por definición, dicha fuerza centrípeta no puede generar trabajo, por lo que

E_{cf} - E_{ci} = 0 \rightarrow E_{cf} = E_{ci}

Indicando que la energía cinética es constante, lo que es lógico cuando uno sostiene que la única velocidad presente es la tangencial cuyo modulo es constante.

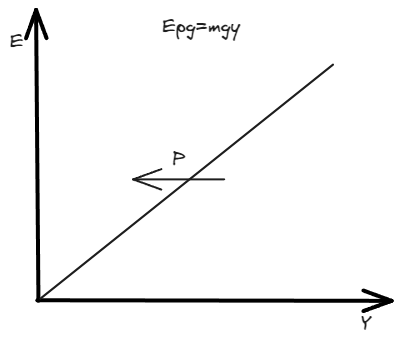
Energía potencial gravitatoria

Si la energía es la capacidad de los sistemas de generar trabajo, entonces los sistemas que solo se encargan de reposicionar objetos y que son capaces de generar trabajo, deben tener algún tipo de energía asociada.

Supongamos por un momento que deseamos elevar un objeto que esta en un punto $A$ en el suelo, y lo elevamos hasta un punto $B$ localizado a una altura $h$ inmediatamente arriba del punto $A$ . Cuando realizamos trabajo para elevar el objeto, también le damos la potencialidad para adquirir energía cineteca una vez que lo soltemos, en otros términos, le estamos entregando energía potencial.

La fuerza encargada de subir el cuerpo debe superar al peso, entonces debemos definir el trabajo realizado por el peso.

W_{peso} = \int_B^A -mg\hat y \space dy \hat y

Al ser colineales la fuerza y el desplazamiento, el trabajo se reduce a:

W_{peso} = -mgh

La energía potencial gravitatoria se define como la energía que posee un objeto debido a su posición en un campo gravitatorio. En el caso del ejemplo anterior, la energía potencial gravitatoria $E_{pg}$ del cuerpo en el punto $B$ es mayor que en el punto $A$ . La diferencia de energía potencial gravitatoria entre dos puntos, $\Delta E_{pg}$ , se puede calcular como:

\Delta E_{pg} = E_{pgB} - E_{pgA} = mgh.

Donde $m$ es la masa del objeto, $g$ es la aceleración debido a la gravedad y $h$ es la diferencia de altura entre los dos puntos.

Por lo dicho hasta el momento, el trabajo del peso se puede definir como:

W_{peso} = - \Delta E_{pg}

Primera ley de conservación de la energía

La energía potencial se puede transformar en energía cinética si el objeto se mueve hacia abajo, y viceversa. En general, la energía total de un sistema se conserva, es decir, la suma de la energía cinética y la energía potencial es constante. La relación entre ambas se puede lograr mediante las definiciones del trabajo que realizan cada una. Sea $W =\Delta E_c$ y $W_{peso} = - \Delta E_{pg}$ , podemos plantear que $-\Delta E_{pg} =\Delta E_c$ , esto significa que son iguales en magnitud pero de signos opuestas.

Finalmente definimos a la energía mecánica como la suma entre la energía cinética y la energía potencial gravitatoria de un sistema.

E_m = E_c + E_{pg}

Si la energía mecánica se conserva, es decir, que solo actúan fuerzas conservativas, entonces podemos decir que el trabajo neto realizado sobre el sistema es igual a la variación de su energía mecánica. Es decir:

W_{neto} = \Delta E_m = \Delta E_c + \Delta E_{pg} = 0

Esta expresión es conocida como la ley de conservación de la energía, donde $W_{neto}$ es el trabajo neto y $\Delta E_m$ es la variación de la energía mecánica del sistema. Este concepto es muy importante en la resolución de problemas de mecánica, ya que permite calcular la velocidad o la altura final de un objeto en movimiento sin necesidad de conocer todos los detalles del proceso.

Energía potencial asociada

En general, si la fuerza aplicada sobre un cuerpo es una fuerza conservativa, lo que implica que solo depende de su posición, entonces podemos decir que existe una energía potencial asociada que se puede expresar como:

\begin{split} \Delta E_{p_{conservativa}} &= -W_{F_{conservativa}}\\ &= -\int\limits_{\vec r_i}^{\vec r_f} \vec F_{conservativa} \cdot d \vec r \end{split}

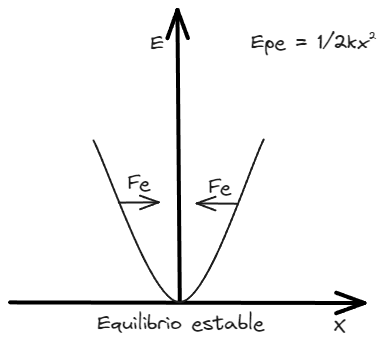
Energía potencial elástica

La energía potencial elástica se define como la energía que un objeto posee debido a su deformación elástica. Esta energía se almacena en el objeto cuando se aplica una fuerza que lo deforma y se libera cuando el objeto vuelve a su forma original. En el caso de la fuerza elástica que se define como $\vec F_e = -kx\hat x$ , la energía potencial elástica se puede calcular como:

\begin{split} \Delta E_{PE} &= - \int\limits_{x_i}^{x_f} -kx\hat x \cdot dx \hat x\\ &= k\frac{x_f^2 - x_i^2}{2}\\ &= \frac{kx_f^2}{2} - \frac{kx_i^2}{2} \end{split}

Primera ley de conservación de la energía general

En un sistema sometido por diversas fuerzas que pueden ser conservativas como no conservativas, podemos calcular el trabajo realizado en dicho sistema entre dos puntos $A,B$ como:

W_{A,B} = W_{A,B}^C + W_{A,B}^{NC}

Donde $W_{A,B}^C$ es el trabajo realizado por las fuerzas conservativas, mientras que $W_{A,B}^{NC}$ es el ejercido por fuerzas no conservativas. Sabiendo que $W_{A,B} = E_{cf} - E_{ci}$ y que $W_{A,B}^C = -(E_{PB} - E_{PA})$ , podemos caracterizar a $W_{A,B}^{NC}$ como:

\begin{split} W_{A,B}^{NC} &= W_{A,B} - W_{A,B}^C\\ &= (E_{cf} - E_{ci}) - (-(E_{PB} - E_{PA}))\\ &= (E_{cf} - E_{ci}) + (E_{PB} - E_{PA}) \\ &= (E_{cf} + E_{PB}) - (E_{ci} + E_{PA}) \end{split}

La igualdad que veremos a continuación es la que llamamos Ley de conservación de la energía:

W_{A,B}^{NC} = \Delta E_{m_{A,B}}

Con esta formula vamos a poder calcular los estados cinéticos de un cuerpo sin tener que pasar por dinámica del mismo, solo mediante sus variaciones.

Aplicación practica

Observar que la energía potencial se describe en términos de su variación entre dos estados y su relación con el trabajo. Esto no es casual, dado que las definiciones absolutas son poco practicas al momento de resolver problemas. En su lugar, las variaciones nos permiten elegir un estado inicial para el cual, la energía potencial en esas condiciones vale cero y calcular como su variación en comparación con otro estado puede producir trabajo.

Para que lo podamos entender, algo similar ocurre cuando uno elige un sistema de referencia para el análisis del movimiento de un cuerpo. Al igual que en esos casos, nosotros podemos decidir donde colocar nuestro eje de coordenadas (o potencial en cero) tal que facilite nuestro labor.

Supongamos por un momento un péndulo ideal de longitud $l$ cuya máxima amplitud es $\theta_{max}$ , punto en el cual la velocidad del cuerpo puntual es cero. Nuestra pregunta es ¿Cuál es la velocidad del péndulo cuando llega a la posición de equilibrio?.

La respuesta puede tener lugar en un análisis sobre la dinámica del sistema. De hecho, ínsito al lector a realizar ese ejercicio. Pero a continuación veremos un segundo procedimiento mucho más practico en comparación.

En primer lugar, revisamos que fuerzas actúan en el sistema. Recordemos que la ley de conservación de la energía habla sobre

W_{A,B}^{NC} = \Delta E_{m_{A,B}}

Por ende, lo primero que se debe determinar es si las fuerzas aplicadas son conservativas o no. El peso ya dijimos que era una fuerza conservativa, en cambio, la tensión es una fuerza no conservativa, pero no produce trabajo ya que es siempre perpendicular a la trayectoria, por tanto, la energía se conserva $\Delta E_{m_{A,B}}= 0$ .

Untitled

Para este caso, decidimos que el punto de equilibrio es el estado de potencial igual a cero o punto $A$ , con lo que el problema se resuelve de la siguiente manera

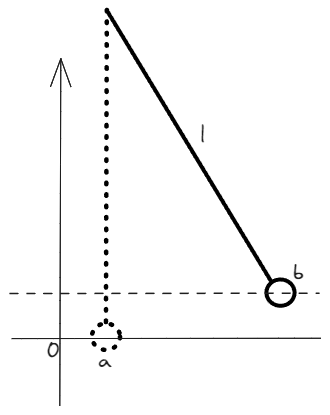
Untitled

\begin{split} \Delta E_{m_{a,b}}&= 0\\ (E_{cb}+E_{pb}) - (E_{ca}+E_{pa}) & = 0\\ (E_{cb}+E_{pb}) &= (E_{ca}+E_{pa})\\ E_{ca} &= E_{pb}\\ \frac{1}{2}mv_a^2 &= mgh_b\\ \frac{1}{2}v_a^2 &= gh_b\\ \frac{1}{2}v_a^2 &= gl(1-cos \theta_{max})\\ v_a &= \sqrt{2gl(1-cos \theta_{max})} \end{split}

¿Qué hubiese ocurrido si cambiamos el punto de potencial igual a cero? Spoiler, da lo mismo.

Diagramas de energía

Los diagramas a los que se hace referencia en el titulo de esta sección, son representaciones comparativas de la evolución en función del movimiento, de las distintas energías, en general, conservativas, capaces de producir trabajo en un sistema.

En general, en el eje vertical se colocara a las energías (mecánica, cinética, elástica, etc.), en función de la posición. Si bien, en los diagramas solo se visualizaran movimientos unidimensionales, se puede extrapolar a más dimensiones sin ningún problema.

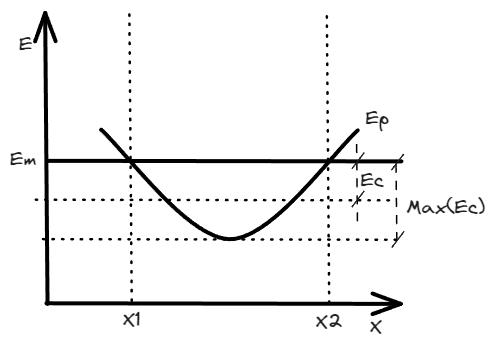
Untitled

Del diagrama que se encuentra arriba podemos obtener mucha información. Lo primero que podemos destacar es algo obvio: la energía mecánica es constante.

En segundo lugar, están los puntos $x_1, x_2$ , donde se igualan la energía mecánica y la potencial $Em = Ep$ , por lo que se puede deducir que la energía cinética es cero, lo que solo ocurre cuando la velocidad es cero, es decir que, el cuerpo en estudio esta quieto en esas dos posiciones.

Una tercera observación esta ligado a $E_c = E_m - E_p$ y como lo podemos ver reflejado gráficamente en el diagrama. Es mas, podemos ver cuando la energía cinética alcanza su máximo valor.

Lo que nunca llegaremos a ver es energía cinética negativa. No es posible ni física, ni aritméticamente, por lo que $E_m \geq E_p$ . Es así que los puntos $x_1, x_2$ son conocidos como puntos de retorno. El cuerpo en estudio simplemente no puede pasar de esos dos limites, al menos no con la energía que posee. Seria necesaria la intervención de una fuerza que introduzca energía al sistema, elevando al “vara” de la energía mecánica y haciendo posible que el cuerpo rompa las barreras de potencial impuestas. Al intervalo $(x_1, x_2)$ se lo conoce como pozo de potencial.

A los movimientos cuyo diagrama de energía hacen parecer que el cuerpo esta encerrado entre dos puntos de retorno, se los conoce como movimientos ligados. Un ejemplo puede ser el caso de un sistema masa-resorte.

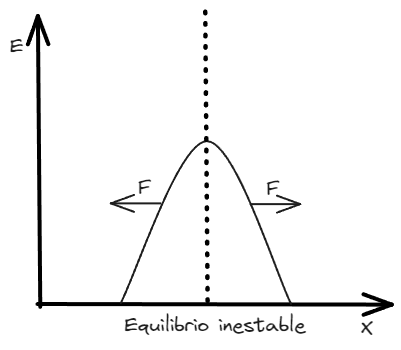
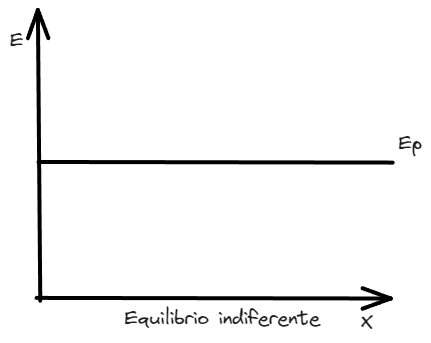
Si recordamos que $\Delta E_p = - \int \vec F \cdot d\vec r$ , entonces es claro que podemos plantear la derivada en ambos términos y expresar la fuerza conservativa como

|\vec F| = -\frac{dE_p}{dx}

Esto puede ser de mucha ayuda para explicar el comportamiento de la fuerza en función de la energía potencial asociada. Podemos encontrar puntos de equilibrio, máximos o mínimos de dicha fuerza.

La expresión $|\vec F| = -\frac{dE_p}{dx}$ no hace mas que profundizar el concepto de puntos de retorno. Si revisamos un momento nuestro ejemplo, en le punto $x_1$ , $\frac{dE_p}{dx} < 0$ , por lo que $\vec F$ es positiva, ósea que, empuja al cuerpo nuevamente al pozo de potencial. Algo similar ocurre en $x_2$ .

Veamos algunos ejemplos del comportamiento de las fuerzas de acuerdo a la energía potencial asociada.

Untitled