Guía 2 - Dinámica: Leyes de Newton, problemas simples. Fuerzas de vinculo

Dinámica

La dinámica es la parte de la física que se encarga del estudio de las causas que producen el movimiento de los cuerpos y de las leyes que lo rigen, especialmente las leyes de Newton. Por eso, comenzaremos a trabajar con interacciones, lo que nos motiva a definir la principal magnitud de la dinámica; La fuerza.

En física, la fuerza se define como cualquier influencia que pueda cambiar el estado de movimiento o la forma de un objeto. Es decir, la fuerza es una magnitud física que puede producir una aceleración en un objeto o deformarlo.

La fuerza se mide en unidades de newton (N) en el Sistema Internacional de Unidades (SI). Una newton es la fuerza necesaria para producir una aceleración de 1 metro por segundo cuadrado en un objeto con una masa de 1 kilogramo.

Existen diferentes tipos de fuerzas en la física, como la fuerza de la gravedad, la fuerza eléctrica, la fuerza magnética, la fuerza de fricción, la fuerza normal, entre otras. Cada tipo de fuerza tiene sus propias características y se rige por sus propias leyes físicas.

Para el estudio de la dinámica de los objetos, precisamos suponer un ambiente controlado, donde solo ocurran interacciones controladas sobre objetos aislados.

Por ejemplo: Si deseamos estudiar la caída de un cuerpo puntual, podemos suponer un rozamiento con el aire despreciable, por lo que solo la fuerza gravitatoria es la que actúa.

Otra hipótesis que planteamos es que ante la ausencia de interacciones, el cuerpo de estudia mantiene una velocidad constante.

Primera ley de Newton: Principio de inercia

La primera ley de Newton, también conocida como la ley de inercia, establece que un objeto en reposo permanecerá en reposo y un objeto en movimiento seguirá moviéndose con velocidad constante en línea recta, si la sumatoria de las fuerzas externas que actúan sobre un cuerpo se cancelan entre si, $\sum \vec F_{externas} = 0$. Observar que las fuerzas poseen una magnitud y una dirección, por tanto, son vectores.

Por ejemplo, si sostenemos un objeto con nuestra mano, este se mantendrá en reposo dado que actúan fuerzas que se cancelan entre si. La primera dada por la fuerza de gravedad que atrae al objeto hacia la tierra, y la segunda dada por la fuerza que ejerce uno para sostener el mencionado objeto.

Segunda ley de Newton: Principio de masa

¿Cuánto esfuerzo se requiere para modificar el estado de objeto en MRU? Supongamos que una pelota de tenis se mueve hacia nosotros con una velocidad de $30 \frac{m}{s}$ constante. Detener a esa pelota con la mano no “cuesta” mucho. Pero, que pasa con una piedra que viaja a la misma velocidad. Notaremos por el dolor en nuestra extremidad, que efectivamente se requirió más esfuerzo detener la piedra que la pelota.

Este ejemplo nos transmite de forma muy coloquial el concepto de inercia. Podemos decir que la pelota tenia una menor inercia en comparación con la piedra debido al “esfuerzo” que se requirió para cambiar su estado. La inercia de un cuerpo esta dada por otra propiedad que llamamos masa. A mayor inercia, mayor masa, e inversamente.

Si quisiéramos cuantificar la inercia de un objeto, podríamos usar un resorte, para que en base a su longitud antes y después de chocar con el objeto, asignar una medida de inercia y de masa.

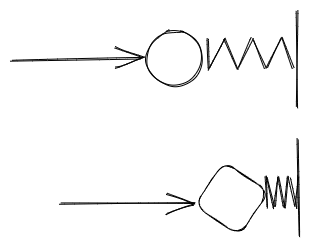
A este experimento se lo conoce como “pesar” un objeto. Pesar un cuerpo no es más que cuantificar el esfuerzo requerido para detener un objeto que cae hacia la tierra.

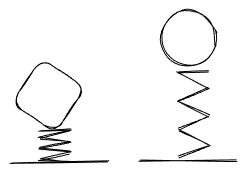
Entonces, un objeto con mayor masa requerirá de mayor fuerza para ser detenido que un objeto de menor masa. Esto nos indique hay una relación entre la fuerza y la masa, $|\vec F| \propto m$.

Ahora comparemos dos pelotas que viajan a distintas velocidades. Nuestra intuición nos dice que la pelota que viaje a mayor velocidad es la que “costara” más esfuerzo detener.

Por lo que sabemos de cinemática, un objeto solo puede detenerse si existe una aceleración opuesta a su velocidad. Podemos inferir que a mayor velocidad, mayor tiene que ser la aceleración.

Estamos en condiciones de afirmar que existe una relación entre la aceleración requerida para detener un objeto y el esfuerzo necesario, $\vec F \propto \vec a$.

La segunda ley de Newton, también conocida como principio de masa, nos confirma que las fuerzas actuantes sobre un cuerpo, son proporcionales a su aceleración y su masa.

Dado que la fuerza esta dada como producto de masa y aceleración, su unidades serán $kg \frac{m}{s^2}$ o $g \frac{cm}{s^2}$. Un newton ($N$) es equivalente a $1kg \frac{m}{s^2}$, una dyna es equivalente a $1g \frac{cm}{s^2}$.

Sistemas inerciales

Como lo mencionamos al inicio, es importante definir el marco en el cual se ejecutan los experimentos para que las inferencias y los resultados sean validos. La primera ley de Newton nos proporciona ese marco condicionándonos a un sistema de referencia donde no se agregan interacciones de ningún tipo sobre el objeto de estudio.

A estos sistemas aislados y adoptados como de referencia, se los conoce como sistemas inerciales.

Propongamos el peor de los sistemas de referencia para nuestro caso, un tren en movimiento. Si llevásemos a cabo nuestros experimentos dentro de un vagón en movimiento, nada seria valido, dado que continuamente sufriríamos de diversos percances como el tren acelerando o frenando.

Si estamos en un sistemas inercial, entonces la primera ley de Newton se cumple e inversamente. Y si estamos en un sistema inercial, la segunda ley de Newton es valida.

Cantidad de movimiento o impulso lineal

El impulso lineal esta definido como $m \vec v = \vec p$ y se obtiene como parte de la segunda ley de Newton:

En los casos en que la masa de un objeto varié en relación al tiempo, el impulso lineal es una definición que nos permitirá seguir trabajando bajo las leyes de Newton.

Tercera ley de Newton: Principio de interacción

Si dos cuerpos interactúan entre sí, las fuerzas aplicadas serán iguales y opuestas

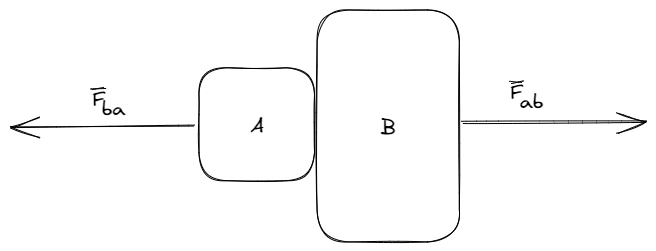
A las fuerzas $\vec F_{a \rightarrow b}$ y $\vec F_{b \rightarrow a}$ las llamamos pares de interacción y actúan sobre cuerpos distintos por lo que no se cancelan. En tanto la fuerza $\vec F_{a \rightarrow b}$ actúa sobre $b$, $F_{b \rightarrow a}$ actúa sobre $a$.

Conclusión

En experimentos donde se evalúen las leyes de Newton, la forma de proceder debería ser la siguiente:

1. Identificar los cuerpos.
2. Identificar fuerzas aplicadas sobre cada cuerpo.
3. Aplicamos las segunda ley de Newton para analizar la dinámica de los cuerpos.

Tipos de fuerza

Atracción gravitatoria o peso

Los cuerpos son atraídos hace la Tierra con una aceleración $\vec a = \vec g$ de magnitud $9,8 \frac{m}{s^2}$. Usando la segunda ley de Newton, puedo encontrar el peso y es $\vec P = m\vec g$.

Vale la pena decir que $\vec P = m\vec g$ es solo una aproximación de la fuerza ejercida por la tierra sobre un cuerpo. Mediciones mas precisas indican que la fuerza gravitatoria se puede calcular como

Donde $M$ es la masa de la Tierra, $m$ es la masa del cuerpo, $r$ es el radio de la Tierra y $G$ es la constante de gravitación universal. Lo que ocurre es que $\vec F_G \approx \vec P$ con objetos cerca de la superficie de la tierra. Esto no es valido cuando analizamos cuerpos que están a mucha distancia o su masa es considerable en comparación a la Tierra.

Fuerzas de contacto

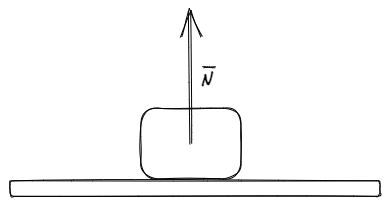
Si tenemos un objeto sobre un superficie, sabemos que el objeto es atraído por la Tierra y tiende a caer, y si no se cae, es porque existe una fuerza perpendicular a la superficie que hace que la aceleración del objeto sea cero. A esa fuerza la llamamos fuerza normal ($\vec N$)

Si tenemos un objeto sobre una superficie que esta sujeto a una soga, la cual es usada para mover el objeto, entonces existe una fuerza que actúa sobre el cuerpo y esta dado por la soga, que puede pensarse como fuerza de tracción o tensión.

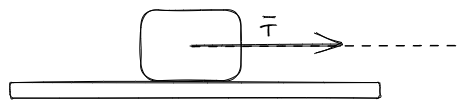
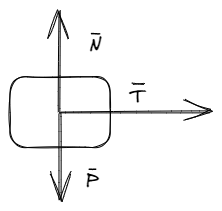
Es común que para visualizar las fuerzas que interactúan sobre un cuerpo se usen los llamados diagramas de cuerpo libre, donde no se dibujan otros cuerpos más que el estudiado y las fuerzas que actúan sobre él.

Cuerpos en equilibrio

Un cuerpo esta en equilibrio si $\sum \vec F_{externas} = 0$, por ejemplo, un cuerpo apoyado sobre una mesa esta en equilibrio, a pesar de que actúan sobre el dos fuerzas, el peso y la normal. Pues bien, si esta en equilibrio entonces $\vec N - \vec P = 0$, lo que $\vec N = \vec P$. De esta forma, podemos resolver múltiples problemas.

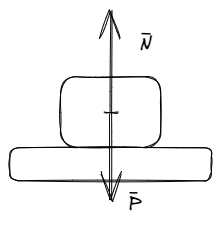
Cuerpos Acelerados

¿Qué pasa si el plano sobre el que esta apoyado el cuerpo esta inclinado? ¿Qué pasa si alguien empuja o tira de un cuerpo a través de una soga? En cualquiera de esos casos, lo que tenemos son cuerpos cuya aceleración es distinta de cero.

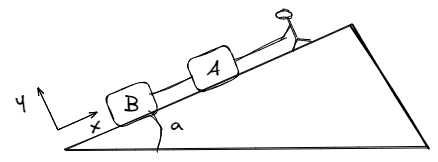
Para nuestro ejemplo, proponemos dos cuerpos atados mediante una soga tal como lo muestra la figura. El cuerpo $A$ es a su vez, elevado a través del plano mediante una soga que es tirada por una persona.

Procedemos tal cual como se planteo en secciones anteriores con algunos añadidos

• Identificamos los cuerpos.
• Seleccionamos un sistema de referencia conveniente.
• Identificar fuerzas aplicadas sobre cada cuerpo.
• Aplicamos las segunda ley de Newton para analizar la dinámica de los cuerpos.
• Escribir las condiciones de vinculo que relacionan las posiciones de cada cuerpo.
• Hallar la aceleración de cada cuerpo y la tensión de los hilos en función de las masas y la gravedad.

Aplicando la segunda ley de Newton

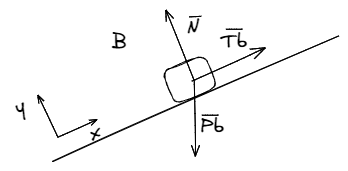
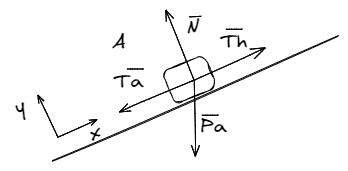
La selección del sistema de referencia no es algo trivial. La regla general es que los ejes sigan la dirección del movimiento. De esa forma, se facilita la aplicación de la segunda ley de Newton. Para nuestro ejemplo, el sistema de referencia tiene la misma inclinación que la superficie de apoyo.

Bajo estas condiciones, el movimiento de los cuerpos puede ser analizado como un movimiento acelerado unidimensional. Planteamos las ecuaciones de Newton sobre los cuerpos $B$ y $A$.

Donde $P_{Bx}$ es la proyección del peso del cuerpo $B$ sobre el eje $x$, idénticamente con $P_{Ax}$. Observar que estamos trabajando con componentes y no con vectores.

Los resultados del análisis dependen del sistema de referencia seleccionado, por lo que no es de extrañar encontrar diferencias entre las soluciones para un mismo caso.

¿Cuál es el papel que juega la cuerda en este sistema?

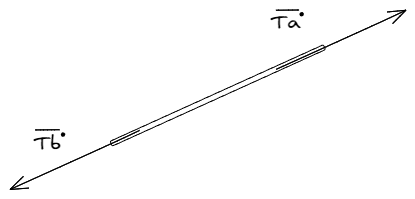
Vamos a suponer que la soga es un cuerpo con masa despreciable para cualquier instante de tiempo. Estas hipótesis de trabajo tiene varias consecuencias y para demostrarlas aplicaremos la segunda ley de Newton:

Pero como la masa de la soga es despreciable, se puede decir que

Aplicando la tercer ley de Newton, podemos obtener el siguiente resultado:

Esto quiere decir que una soga de masa tendiente a cero tiene la propiedad de transmitir las tensiones entre los cuerpos que conecta.

Condición de vinculo y sus ecuaciones

Para determinar la aceleración del sistema, vamos a proponer la siguiente hipótesis: La soga que une ambos cuerpos es inextensible.

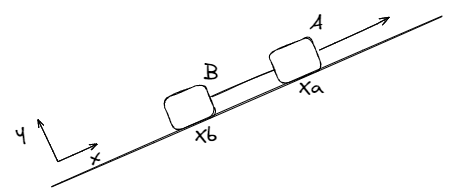
Si la soga es inextensible, entonces la distancia $C$ entre los cuerpos se mantiene constante para todo instante de tiempo, $x_B - x_A = C$. Si derivamos esta expresión, obtenemos lo siguiente:

Lo que implica que las velocidades de ambos cuerpo son iguales. Y si volvemos a derivar la expresión, llegamos al siguiente resultado:

Las aceleraciones son iguales tanto en magnitud como en sentido.

¿Qué ocurre en sistemas más complejos?

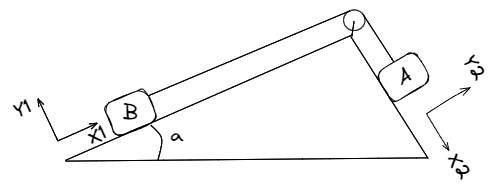
Sea $L$ la longitud total de la soga que une los cuerpo $A$ y $B$, $x_b$, $x_p$ la posición del cuerpo $B$ y la polea respecto del primer sistema de referencia, $x_a$, $x_p \prime$ la posición del cuerpo $A$ y la polea respecto del segundo sistema de referencia, podemos plantear la siguiente ecuación de vinculo

Tanto $xp$ como $xp \prime$, son constantes, por lo que si derivamos la ecuación, se concluye que:

Una segunda derivada establece las relaciones entre las aceleraciones, lo que además, puede permitir alcanzar ecuaciones de movimiento de cada cuerpo.

Que las aceleraciones de ambos cuerpos sean iguales tanto en magnitud como en sentido, es acorde a los sistemas de referencia propuestos. Si el cuerpo $B$ asciende por el plano inclinado, en sentido de $x_1$, el cuerpo $A$ descenderá por el plano en el mismo sentido que $x_2$.

La igualdad $\ddot{x_b} = \ddot{x_a}$ permite relacionar los sistemas de referencias propuestos, haciendo posible reemplazarlos en las ecuaciones de Newton de cada cuerpo.

La aceleración en función de las masas

Volvamos a nuestro ejemplo inicial con las ecuaciones y los resultados obtenidos hasta el momento.

Si sumamos las ecuaciones $B_x$ y $A_x$ podemos generar la siguiente ecuación

Lo que nos indica que la aceleración del sistema es igual a:

Fuerzas de acción y reacción en sistemas con poleas

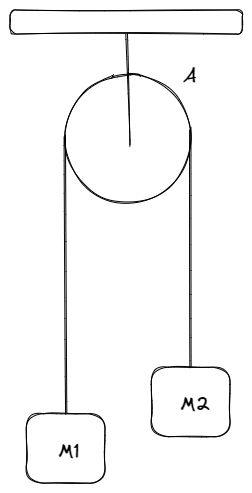
Para esta sección, no analizaremos la dinámica de las masas, sino lo que ocurre hacia adentro de la soga que sostiene los cuerpos y la polea que retiene a la soga. Diremos que la polea no posee masa y no existe fricción alguna con la soga.

¿Qué fuerzas se aplican sobre la polea?¿Y sobre la soga?¿Cual es el sistema de referencia más conveniente para analizar estos cuerpos? Aunque no lo parezcan, estas preguntas no son triviales y traerán mas de un dolor de cabeza.

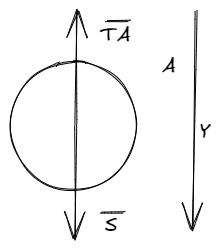
Sobre la polea se aplican dos fuerzas: $\vec{T_a}$ que es la fuerza del soporte que lo sostiene y $\vec S$ que es la fuerza que ejerce la soga sobre él. Como ambas fuerzas ocurren sobre una misma dirección pero en sentido contrario, lo más conveniente es elegir un sistema de referencia paralelo a las fuerzas, lo que nos brinda la posibilidad de escribir las ecuaciones de Newton en una sola componente

Dado que la polea no posee masa, esto resulta en:

¿Cuál es el valor de $S$? Para responder a esto, nos valemos de su par de acción aplicado sobre la soga.

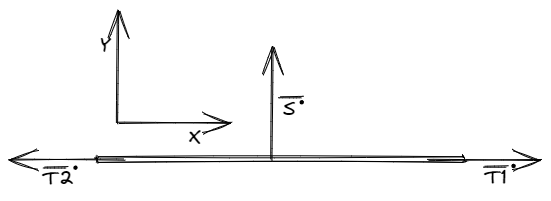
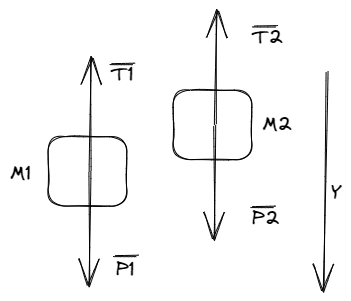
Sobre la soga se aplican tres fuerzas que son a su vez pares de reacción de fuerzas aplicadas sobre las masas y la polea. Observar que la fuerza $\vec S'$ es perpendicular al punto de contacto con la polea, similar a lo que ocurre con la normal.

Aplicando la segunda ley de Newton y sabiendo que la masa de la cuerda es tendiente a cero, obtenemos la siguiente ecuación

Los corolarios de esta ecuación son evidentes

Dado que $\vec T_1$, $\vec T_2$ y $\vec S$ actúan siguiendo un mismo eje, se puede generar las siguientes equivalencias

Ya habíamos analizado el valor de las tensiones en una cuerda, pero lo volvemos a traer. Si analizamos el eje $x$ de nuestro sistema de ecuaciones, se concluye que:

Con lo que podemos concluir que