Guía 3 - Oscilaciones

Fuerzas dependientes de la posición

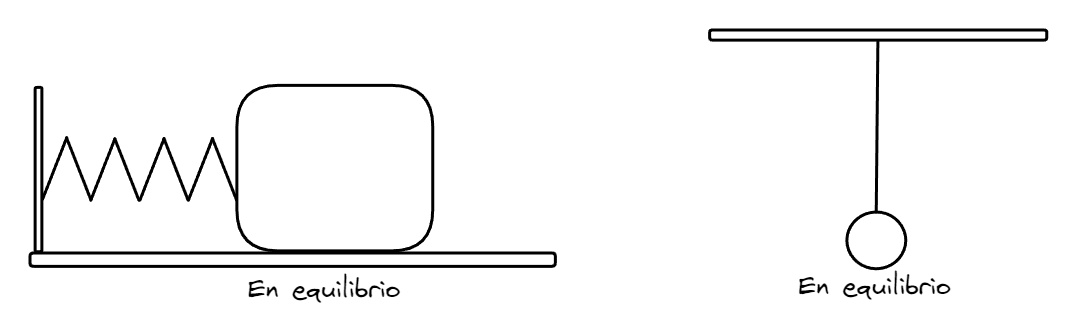
Para analizar fuerzas dependientes de la posición, veremos dos casos representativos. Por un lado, tenemos un cuerpo de masa $m$ que esta unido a una pared mediante un resorte. Por el otro, existe un cuerpo de masa $m$ que esta sujeto a un techo mediante una cuerda de largo $l$. En ambos casos existe un estado de equilibrio, pero en el momento en que estos cuerpos se separen de ese estado, aparecerá una fuerza que intentara devolver al objeto a su estado original. A estas fuerzas se las puede definir como fuerzas restitutivas. En el caso del resorte, trabajaremos con fuerzas elásticas, mientras en el péndula, la fuerza restitutiva será el propio peso cuerpo.

Podemos decir que ambos casos dan lugar a oscilaciones o movimientos de vaivén cuando se encuentran fuera de su estado de equilibrio. Al mismo tiempo, se puede reconocer que las fuerzas implicadas en la recomposición del estado se incrementan en proporción de la distancia a la que se encuentren de su posición original.

Primer caso: Resorte

Sea un cuerpo de masa $m$ que esta unido a una pared mediante un resorte cuya longitud en reposo (sin tracción ni compresión) es $l_o$.

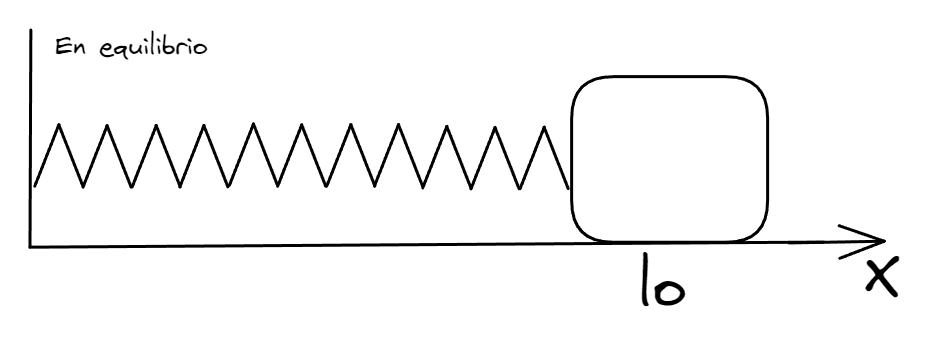
Si adoptamos un sistema de referencia unidimensional, cuyo origen es la pared, podemos decir que el cuerpo localizado en el punto $l_0$ esta en equilibrio.

Existen tres posibles situaciones, si el cuerpo es movido a una posición $x > l_0$, la fuerza restitutiva $\vec F_e$ será negativa, si por el contrario, la nueva posición es $x < l_0$, la fuerza $\vec F_e$ será claramente positiva. Si $x=l_0$, entonces $\vec F_e = 0$.

Podemos plantearnos, por experiencia, que $|\vec F_e|$ se incrementa en la medida que $|\Delta x | = |x-l_0|$ también lo hace, entonces $|\vec F_e| \propto |\Delta x|$. Si decimos que $\Delta x$ es muy pequeño tal que la proporción lineal entre la fuerza y $\Delta x$, es la que prevalece por encima de otras posibles dependencias, entonces $F_e = k\Delta x$, con $k>0$ constante. Pero hay un problema, y es que si $x > l_0$, entonces $\Delta x > 0$, contrario al signo de la fuerza en esta misma situación. Para remediar esto, diremos que

Esta relación lineal entre la fuerza de estiramiento y la posición del cuerpo, se conoce como la Ley de Hooke y es valida para $\Delta x$ muy pequeños, tal que no se deforme el resorte ni ninguna de sus propiedades. En algunos libros se dirá que $\Delta x$ no debe superar al limite elástico, punto en el cual, el resorte no puede volver a su estado original.

Si el origen de nuestro sistema de referencia lo colocamos sobre $l_0$, la representación de $\vec F_e$ cambia, y de hecho, es la que se usa comúnmente.

En el sistema MKS, el coeficiente $k$ tiene unidades tanto de fuerza, como de longitud, por lo que no es de extrañar que $[k] = \frac{N}{m}$.

Ecuación de movimiento

Volvamos al caso inicial, sea un cuerpo de masa $m$ que esta unido a una pared mediante un resorte cuya longitud en reposo es $l_o$. No existe rozamiento con la superficies de contacto y el cuerpo no esta en equilibrio. Analicemos las fuerzas que pueden interactuar con el cuerpo.

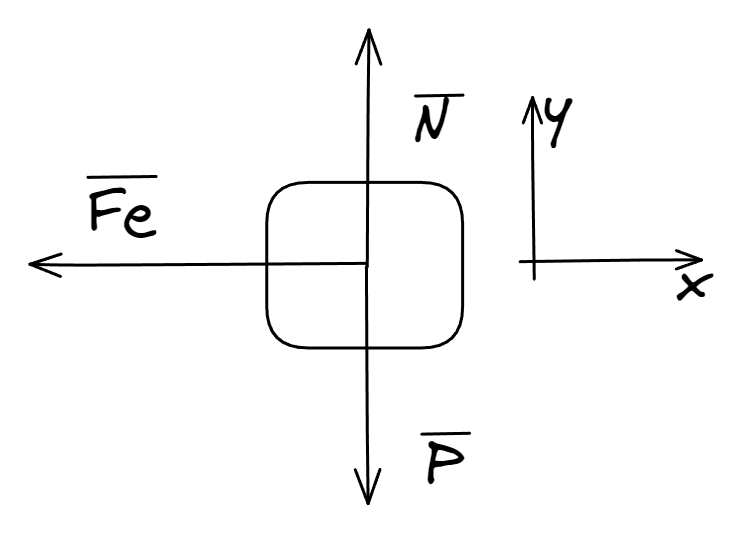
En principio, la fuerza $\vec F_e$ es la única capaz de imponer aceleración al cuerpo, por lo que solo analizaremos el eje $x$. Entonces

Para poder obtener las ecuaciones de movimiento del cuerpo, debemos resolver la ecuación diferencial homogénea de segundo orden

Para resolver esta ecuación partimos de su ecuación característica asociada $r^2 + \frac{k}{m} = 0$ cuyas raíces complejas son $i\sqrt \frac{k}{m}$ y $-i\sqrt \frac{k}{m}$, por lo que las soluciones posibles parten de las siguientes expresiones

Cuando afirmamos que las soluciones posibles parten de las expresiones dadas, es porque podemos multiplicar o sumar constantes que serán anulados en derivadas, manteniendo el carácter de solución. Si aplicamos dichas expresiones generales a condiciones propias del caso que tratamos, es decir, condiciones propias de la física y del mundo real, llegamos a que la familia de soluciones que mejor describe lo observado es:

Donde $\omega_0 = \sqrt \frac{k}{m}$, $A, \varphi_0$ constantes. En particular, se denomina como fase a $\omega_0 + \varphi_0$ y fase inicial a $\varphi_0$. Por el otro lado, a la constante $A$ se la llama amplitud, mientras que a $\omega_0$ se lo conoce como frecuencia angular.

¿Qué representa cada una de estas constantes? Si realizamos un grafico de la posición en función del tiempo con un $\varphi = 0$ y con un sistema referencia centrado en $l_0$, tal cual se planteo hace un tiempo. La constante $A$ representa las posiciones máximas y mínimas alcanzadas por el resorte y el cuerpo puntual. En términos de la función formada por la función $x$, es la amplitud de la onda senoidal.

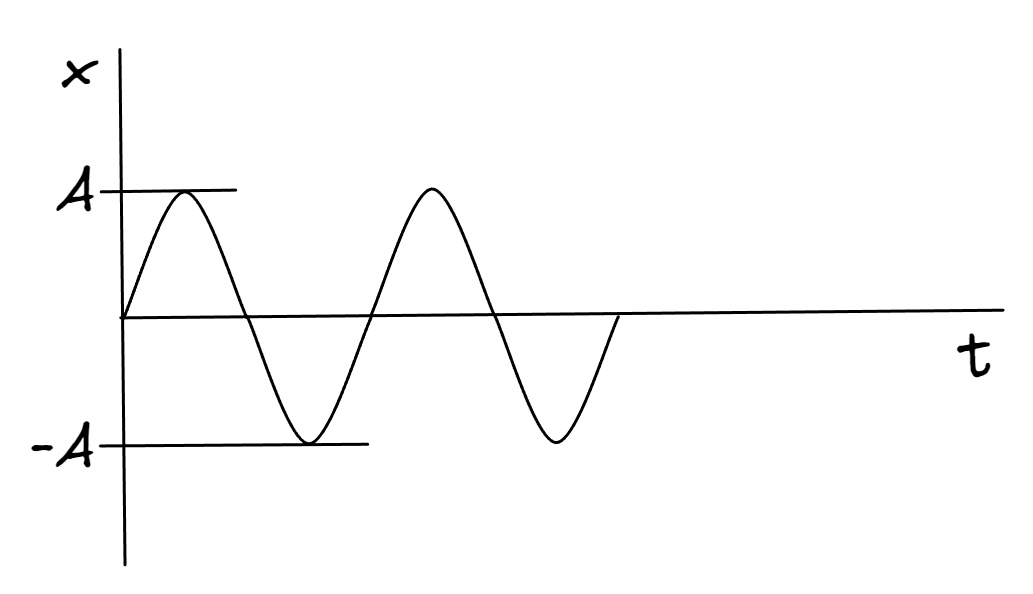
Por otro lado, $\varphi_0$ representa el instante en que inicia el movimiento del resorte y por tanto, un corrimiento en la onda senoidal. Algo a mencionar, y es que si $\varphi < 0$, el corrimiento será hacia la derecha, por el contrario, si $\varphi >0$ el corrimiento será hacia la izquierda. Esto es fácil de ver con un ejemplo, si $\varphi = -\frac{\pi}{2}$, entonces la onda senoidal comenzara cuando $\omega_0 t - \frac{\pi}{2} = 0$ , y esto ocurre con un $t = \frac{\pi}{\omega_02}$, es decir, en un instante positivo.

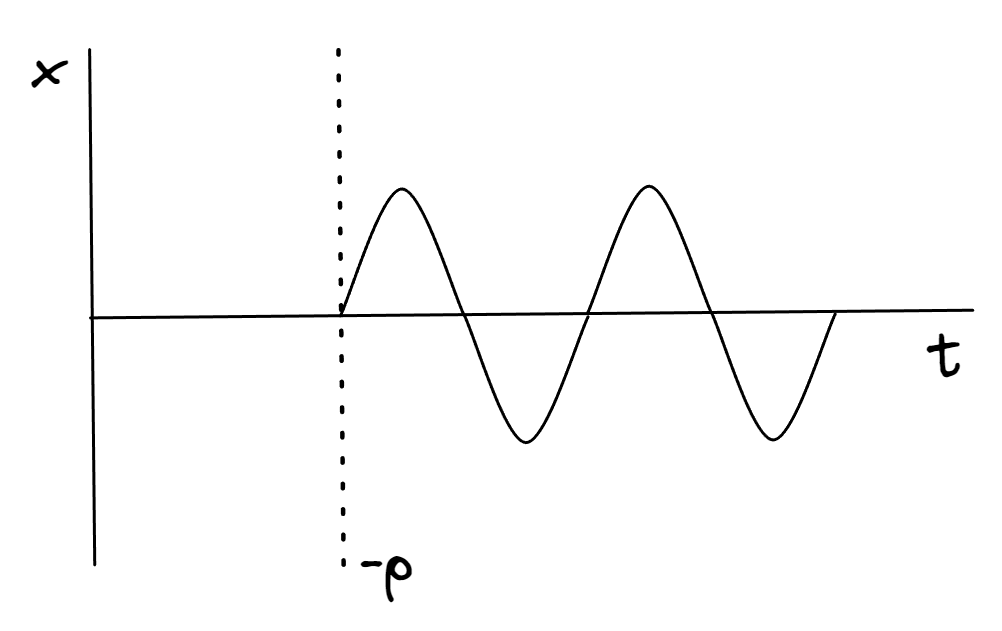
Tanto $A$ como $\varphi_0$ dependen de las condiciones iniciales del problema y no de la fuerza. En cambio, $\omega_0$ depende de la masa del cuerpo y del resorte, ambas propias de la dinámica. Para estudiar las implicancias de $\omega_0$ en el movimiento del cuerpo es necesario hacer algunas observaciones.

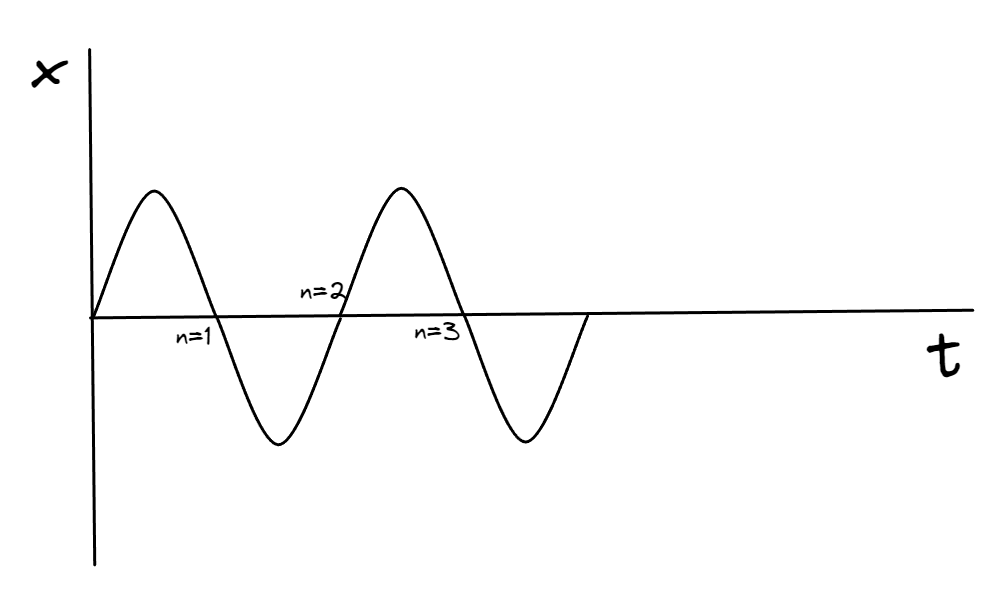
Dado que solo se aplica una fuerza sobre el cuerpo, el movimiento que se observa en las graficas es periódico y suave. A este tipo de comportamiento se lo conoce como movimiento armónico simple o MAS por sus siglas. Suponiendo un $\varphi_0 = 0$, se puede observar que el cuerpo pasa por el origen en lapsos de tiempo igual a $\pi$, es decir que si para un instante de tiempo $t_0$, ocurre que $\omega_0t_0 = n\pi$ con $n\in \N$, entonces $x(t_0) = 0$.

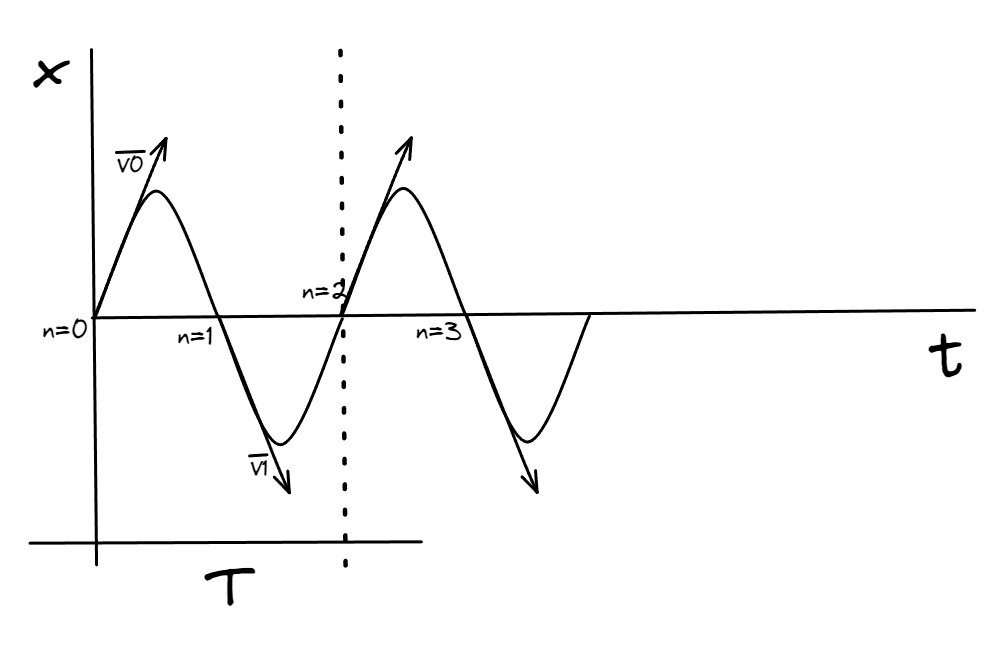
Si bien el cuerpo pasa por el origen, las condiciones cinemáticas pueden variar. Por ejemplo, cuando el cuerpo inicia su movimiento en $n=0$, la velocidad es positiva, en $n=1$, la velocidad es negativa. Recién en $n=2$, la velocidad vuelve a ser positiva, y de hecho, cada $2\pi$, las condiciones cinemáticas se repetirán. A este periodo de tiempo $t$ donde $t=\frac{2\pi}{\omega_0}$ se lo conoce como periodo de oscilación y se lo simboliza con la letra $T=\frac{2\pi}{\omega_0}$.

Ecuación de movimiento según Euler

Si revisamos el apéndice de este articulo, podemos ver que, por la expresión de Euler $e^{ix} = \cos x + i\sin x$, es posible representar a la ecuación de movimiento como:

Segundo caso: Péndulo

Sea un cuerpo de masa $m$ que cuelga de una soga de largo $l$ inextensible y de masa despreciable. El cuerpo describe un movimiento del tipo vaivén cuando no se encuentra en reposo, formando un ángulo $\alpha$ con respecto a su estado de equilibrio.

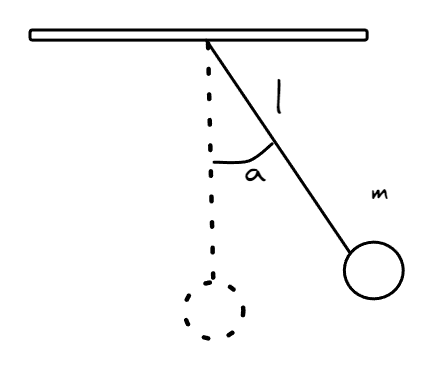
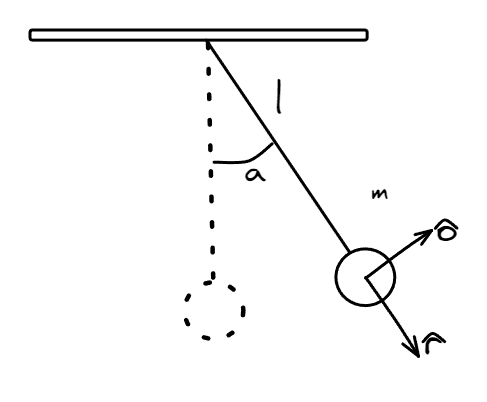
Dado que el movimiento descripto se aproxima a un movimiento del tipo circular, lo más conveniente es usar coordenadas polares. Tener en cuenta las ecuaciones de movimiento demostradas en el apunte de movimiento circular.

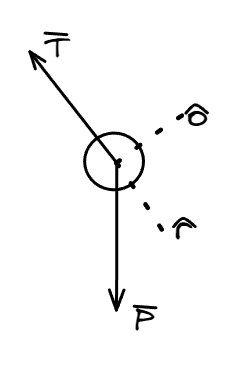
Aplicamos la segunda ley de Newton y obtenemos las siguientes expresiones.

La primera de ellas corresponde a las fuerzas aplicadas en la dirección del versor $\hat r$, y la segunda a las aplicadas en versor $\hat \theta$. Nos vamos a centrar en la segunda expresión para poder determinar la ecuación de movimiento del péndulo. Recordemos que el radio del movimiento es constante por lo que el movimiento va a quedar descripto principalmente por $\theta(t)$.

Lamentablemente, la ecuación diferencial a resolver para obtener $\theta$ no es lineal.

Para hacernos de una solución debemos tomar ciertas hipótesis. Proponemos que el ángulo de desplazamiento, tal que $\sin \theta \approx \theta$. Esto se puede verificar con un polinomio de Taylor de primer orden sobre la función $\sin(x)$ alrededor de cero.

Dicho esto, nuestra ecuación diferencial ahora es:

Por tanto, la solución de la ecuación diferencial es la misma que la vista en la anterior sección con la excepción de que $\omega_0 = \sqrt \frac{g}{l}$.

Una última observación, cuando describimos el periodo para el caso del resorte, se llego a $T=\frac{2\pi}{\omega_0}$ , que aplicado a nuestra situación se vería algo así:

Es decir, que podemos calcular la constante $g$ basándonos en el periodo de un péndulo cuyo ángulo de movimiento es muy pequeño.

Oscilaciones amortiguadas

En los casos anteriores describimos movimientos del tipo armónicos simples perpetuos. Esto quiere decir que, sin la existencia de una fuerza que se oponga al movimiento del cuerpo, este no se detendrá. Pues bien, ahora veremos el caso en el que existe una fuerza que de alguna forma desacelera el cuerpo de estudio.

Sea un objeto de masa $m$ que esta unido a una pared mediante un resorte cuya longitud en reposo (sin tracción ni compresión) es $l_o$. Todo el sistema se encuentra sumergido en un fluido de viscosidad considerable y el rozamiento con las superficies se despreciable.

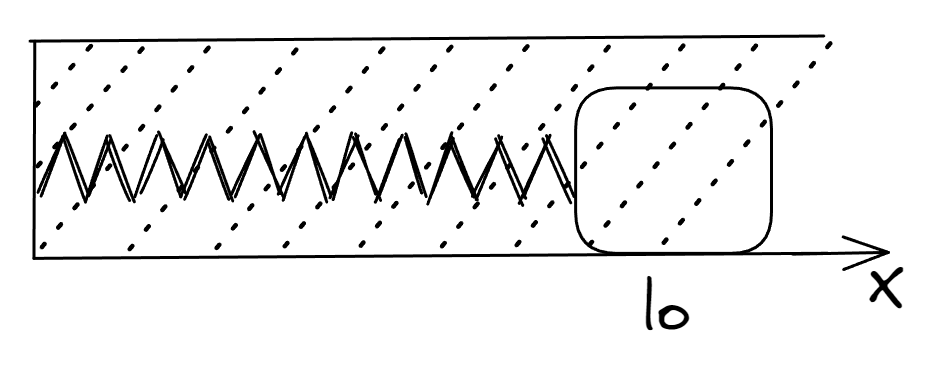
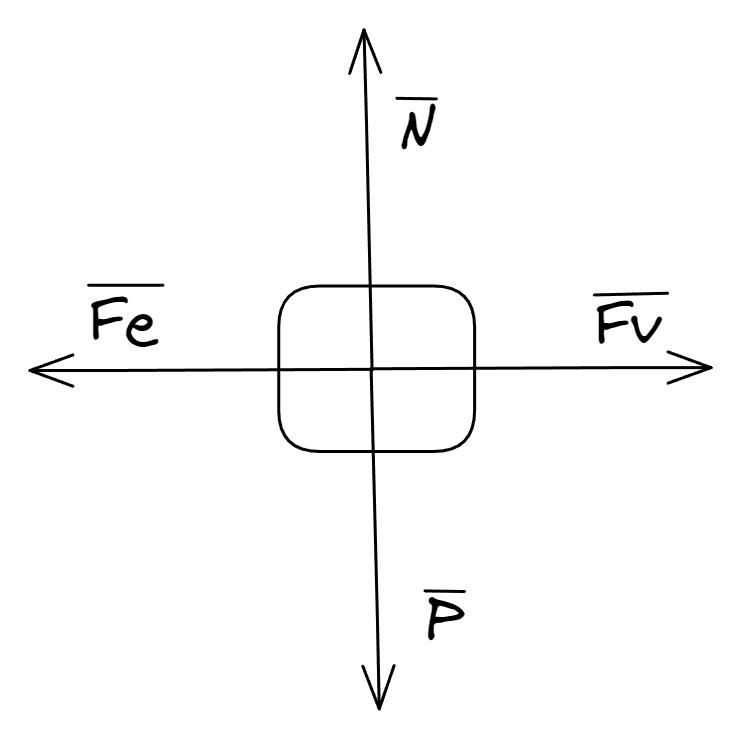
Si consideramos el origen del sistema de referencia en $l_0$, es fácil aplicar la segunda ley de Newton. En este caso nos centraremos en el eje $x$ que es donde puede visualizar el movimiento.

Vemos representada la fuerza viscosa como opuesta a la velocidad del cuerpo (ver apunte sobre rozamiento y viscosidad). Esta ecuación diferencial se puede resolver de la misma forma que lo hicimos en otros casos (ver apéndice sobre ecuaciones diferenciales de segundo orden).

Como en anteriores casos, partimos de la ecuación característica asociada a la ecuación diferencial:

De esta ecuación característica resultan dos posibles soluciones:

Donde $\beta = \frac{b}{2m}$ tiene una clara relación con la fuerza viscosa y $\omega_0^2 = \frac{k}{m}$ que representa la frecuencia natural del resorte, . Lamentablemente, existe un inconveniente $\sqrt{\beta^2 - \omega_0^2}$.

Caso 1: Movimiento sobre amortiguado

Si $\beta^2 - \omega_0^2 > 0$ podemos decir que:

• La fuerza viscosa supera a la fuerza elástica: $\beta^2 > \omega_0^2$ .
• Las raíces de la ecuación característica son reales.

Por tanto, podemos decir que una solución general para este caso es

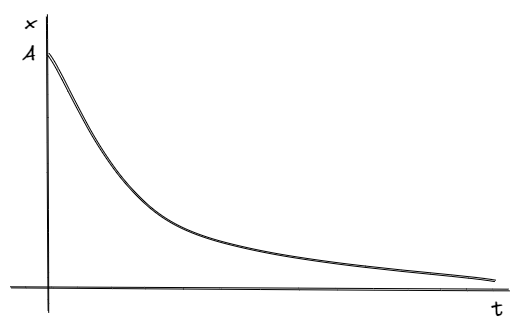
El grafico para la posición en función del tiempo es una exponencial que tiende a cero, indicando que la fuerza elástica intenta devolver al cuerpo a su posición de equilibrio, mientras que la fuerza viscosa no se lo permite.

Caso 2: Amortiguamiento critico

Si $\beta^2 - \omega_0^2 = 0$, es un caso muy especial conocido por amortiguamiento critico, donde la solución general para la ecuación diferencial planteada al inicio es:

Pero este escenario no es frecuente, y cuyo estudio no forma parte de nuestros objetivos.

Caso 3: Movimiento sub amortiguado

Si $\beta^2 - \omega_0^2 < 0$, podemos decir que:

• La fuerza elástica supera a la fuerza viscosa: $\beta^2 < \omega_0^2$ .
• Las raíces de la ecuación característica serán imaginarias: $r_{1,2} = -\beta \pm i\sqrt{\omega_0^2 - \beta^2}$

Si definimos $\omega^\prime$ como $\omega^\prime = \sqrt{\omega_0^2 - \beta^2}$, encontramos que la solución general para este caso es:

En la física clásica, las soluciones imaginarias no existen, por lo que se suele quitar de las expresiones, dejando la parte real. Para este caso, existen tres expresiones reales para la solución.

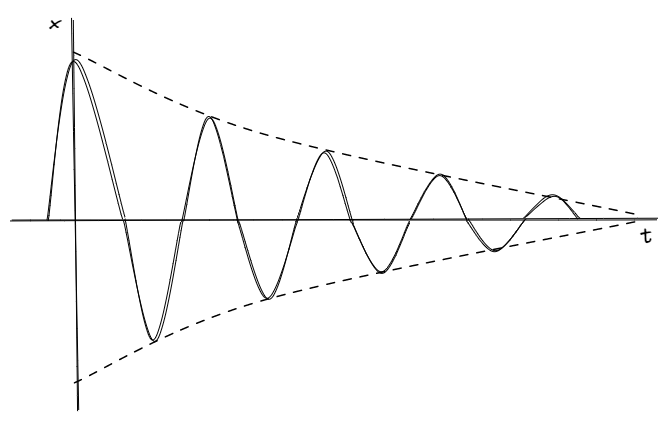
Lo que podemos esperar sobre grafico de estas soluciones es que sea efectivamente una senoidal, pero acotada por una exponencial inversa.

Aproximación al movimiento oscilatorio simple

En diagrama de la posición en función del tiempo, podemos ver como la amplitud de la senoidal cambia en función del tiempo. Mas concretamente por la expresión $A(t) = Ae^{-\beta t}$.

Si $\beta \ll \omega_0$ o lo que es lo mismo $\beta \approx 0$, entonces $\omega^\prime \approx \omega_0$, por lo que $A(t) \approx A$. Si este es el caso, lo que obtenemos es el mismo resultado que conseguimos con el movimiento oscilatorio libre o sin amortiguaciones.

Periodo de un movimiento oscilatorio amortiguado

Como en otros casos, vamos a definir un periodo en el movimiento, que va a estar dado por:

En un escenario donde $\beta \approx 0$, que puede ser el de un resorte moviéndose en un ambiente rodeado de aire básicamente, el periodo se traduce inmediatamente a $T = \frac{2\pi}{\omega_0}$ , que el caso al que ya estamos acostumbrados.

Equilibrio inestable

Un estado de equilibrio inestable es aquel en el que un cuerpo se encuentra en reposo, pero que ante la más mínima perturbación, tiende a alejarse, cada vez con mayor aceleración, de su posición original y no puede volver a su estado inicial.

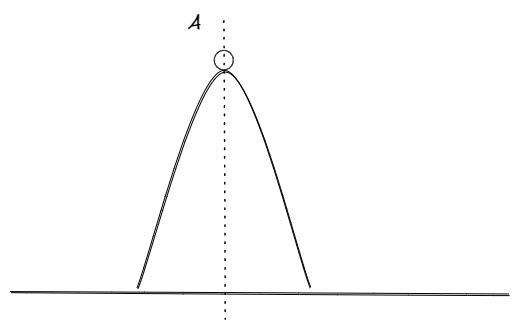
El caso mas simple para ejemplificar un estado de equilibrio inestable es el de una pelota sobre un lomada. Si el cuerpo inicialmente en reposo, es llevado a un punto ligeramente fuera de su posición de equilibrio, comenzara inmediatamente a caer por la pendiente debido a la fuerza de la gravedad.

Por otro lado, un péndulo o un resorte poseen estados de equilibrio estable, donde las alteraciones pueden cambiar su posición, pero las fuerzas restitutivas lo devolverán a su lugar de origen.

Definición de fuerzas cerca del equilibrio estable

Sea una fuerza o resultante de fuerzas, dependiente de la posición $\vec F(x) = F(x)\hat x$, que actúa sobre un cuerpo $m$, que posee un estado de equilibrio estable en $x_{eq}$ donde $F(x_{eq}) = 0$ y cuya primera derivada evaluada en ese mismo punto es negativa, $\dot F(x_{eq}) < 0$.

Uno puede aproximarse a $F(x)$ con un $x$ muy cerca de $x_{eq}$, con una serie de Taylor.

Localizando el origen del sistema de referencia sobre $x_{eq}$, se puede expresar a la fuerza como $F(x) = -Cx$. Aplicando la segunda ley de Newton llegamos a:

Que no es otra cosa mas que un movimiento armónico simple. Por ende, siempre que nos encontremos frente a un sistema en equilibrio estable, podemos aproximar su comportamiento en puntos muy cercanos al punto de equilibrio, mediante como un movimiento armónico simple.

Fuerzas oscilatorias forzadas

Un claro ejemplo de fuerzas oscilatorias forzadas es el caso de un niño que se divierte balanceándose sobre una hamaca mientras que su tutor lo empuja. En este caso, dependiendo de la frecuencia con que se ejerza la fuerza sobre la hamaca, la amplitud oscilante del juego cambiara.

Supongamos el tutor empuja la hamaca una vez por segundo, que es lo que tarda la silla en ir y volver. Pero en un momento, se toma muy en serio su papel y triplica la frecuencia de sus empujes, es decir, ahora lo hace tres veces por segundo. En ese caso, la frecuencia con que se empuja la hamaca es tan alta, que llegará un momento en el que se desincronizará de la oscilación natural del juego y la fuerza que inicialmente lo ayudaba a mantener el ritmo, ahora comenzara a detenerlo, reduciendo la amplitud de movimiento.

En otro escenario, el mismo tutor, decide descansar, y en lugar de empujar la silla una vez por segundo, ahora lo hace cada tres segundos, creando el mismo resultado que en el caso anterior.

En grafico de la amplitud en función de la frecuencia forzada, se pueden observar los dos eventos que se acaban de mencionar.

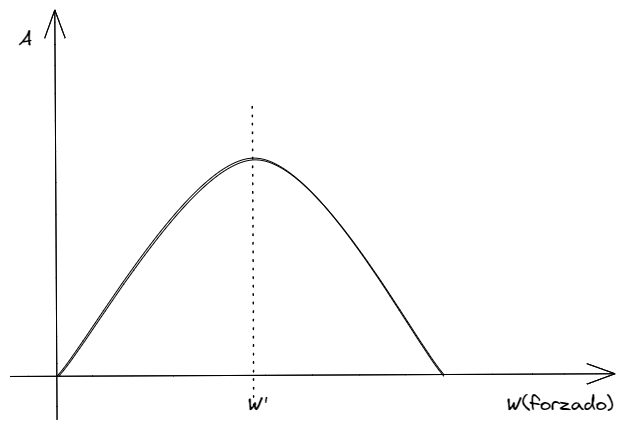
En ese mismo grafico podemos ver como la máxima amplitud de oscilación es logrado en $\omega^\prime = \sqrt{\omega_0^2-\beta^2}$. Este fenómeno que ocurre cuando la oscilación forzada es igual a la oscilación natural se la conoce como resonancia.

Si se obliga a un sistema a oscilar en su frecuencia natural, se maximiza la transferencia de energía entre la fuerza que se ejerce y la que absorbe el sistema. Ejemplos de sistemas hay muchos: instrumentos de cuerda, radio transmisores y receptores, hamacas, etc.