Guía 2 - Dinámica: Rozamiento y viscosidad

Publicado el 4/12/2023

Fuerza de rozamiento estática

La fuerza de rozamiento es una fuerza que se opone al movimiento relativo entre dos superficies que están en contacto. Esta fuerza depende del tipo de superficie y de la fuerza normal que las superficies ejercen entre sí.

No nos debería extrañar que el objeto $B$ no cae con facilidad, aun cuando en el componente $x$ de nuestro sistema de referencia no existe otra fuerza mas que le peso del cuerpo. Esto nos indica que existe otra fuerza a vencer para salir del estado estático y esa es la fuerza de rozamiento estático.

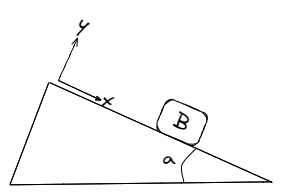
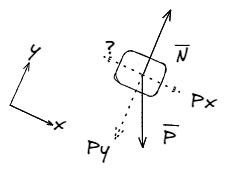
Untitled

Algo que vale la pena mencionar es que la fuerza de rozamiento estático tiene ese nombre porque el objeto aún no cae. Si uno inclino aún mas la superficie hasta un determinado ángulo, que lo llamaremos ángulo limite, el objeto comenzara a resbalarse sobre la superficie, y ese es un caso distinto que merece su propio espacio para ser analizado.

La fuerza de rozamiento se opone al movimiento del objeto. Uno puede empujar un objeto sobre una superficie horizontal y la fuerza de rozamiento aparece en oposición a ese empuje.

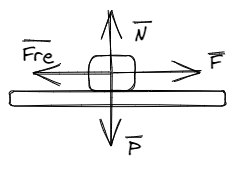
Untitled

Puedo empujar el objeto tanto como sea necesario hasta un punto limite en que la fuerza de rozamiento estático comienza a ceder. En ese instante es que definimos a la fuerza de rozamiento estática como fuerza de rozamiento estática máxima, y se calcula como

F_{re-max} = \mu_e N

El coeficiente adimensional que simbolizamos como $\mu_e$ depende exclusivamente de las superficies en contacto.

Observar que la $F_{re-max}$ depende de $\vec N$ . Esto tiene lógica con el siguiente ejemplo. Supongamos un cuerpo colocado sobre una superficie inclinada, y ejercemos una fuerza perpendicular al plano. Es fácil de imaginar y de probar, que sin importar cuan inclinado se encuentre el plano, si ejercemos la suficiente fuerza, el objeto no se moverá.

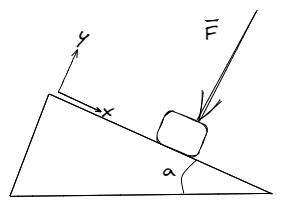
Untitled

Cuando uno ejerce fuerza en forma perpendicular al plano, lo único que incrementa es la fuerza normal o fuerza de contacto. Esto nos hace pensar que la fuerza de rozamiento tiene una componente en la dirección del plano y que se opone al movimiento, y otra componente en dirección de la normal. Este pensamiento esta en lo correcto.

Es fácil calcular $\mu_e$ mediante el ejemplo inicial, donde inclinamos el plano hasta que el objeto finalmente se movía.

Untitled

En el instante anterior a que el objeto se acelere, se alcanzo la $F_{re-max}$ con un determina ángulo $\alpha_l$ . En base a esto calculamos las componentes de la fuerza $\vec P$ y determinamos $\vec N$ .

F_{re-max} = \mu_e N = \mu_e mg\cos\alpha_l

F_{re-max} = mg\sin\alpha_l

\mu_e mg\cos\alpha = mg\sin\alpha \Longrightarrow \mu_e = \frac{\sin\alpha_l}{\cos\alpha_l}

Si nos encontramos en un instante anterior a $F_{re-max}$ , la $F_{re}$ se calcula como

F_{re} = mg\sin\alpha \text{, con } \alpha < \alpha_l.

Fuerza de rozamiento dinámica

Si uno empuja un objeto con una velocidad inicial distinta de cero, con presencia de rozamiento en relación a la superficie de apoyo, eventualmente el objeto se va a detener. Esto quiere decir que existe una fuerza de rozamiento para objeto en movimiento. A esa fuerza la llamaremos fuerza de rozamiento dinámico.

La experiencia nos dice que la $F_{rd} \leq F_{re}$ , es decir, cuesta mucho más poner en movimiento a un objeto que detenerlo.

Por analogía, existe un coeficiente $\mu_d$ tal que

F_{rd} = \mu_d N

Y da la relación entre las fuerzas, podemos decir que $\mu_d \leq \mu_e$ . Tanto la $F_{re}$ , como la $F_{re}$ , se oponen a la tendencia de movimiento. Hablamos de tendencia y no de movimiento, porque en el caso estático, el objeto no se mueve.

Viscosidad

La viscosidad de un fluido es una medida de su resistencia a fluir. Los fluidos con alta viscosidad, como la miel o el aceite espeso, resisten más al flujo que los fluidos de baja viscosidad, como el agua o el aire. La viscosidad es una propiedad importante de los fluidos y se utiliza en muchos contextos, incluyendo la física, la química y la ingeniería.

Nuestro análisis en relación a la viscosidad se va a centrar en la experiencia de un objeto moviéndose dentro de un fluido viscoso a baja velocidad. Esta condición representa una hipótesis de aproximación para la realización de nuestros experimentos. Si el objeto se mueve con una velocidad tal que genera un flujo turbulento dentro del medio en el que se encuentra, no podremos llevar a cabo análisis alguno, ya que un flujo turbulento no puede ser estudiado de forma analítica.

La velocidad del objeto en movimiento debe ser lo suficientemente bajo como para generar un corrimiento de las moléculas del fluido circundante. A este corrimiento de moléculas se lo conoce como flujo laminar.

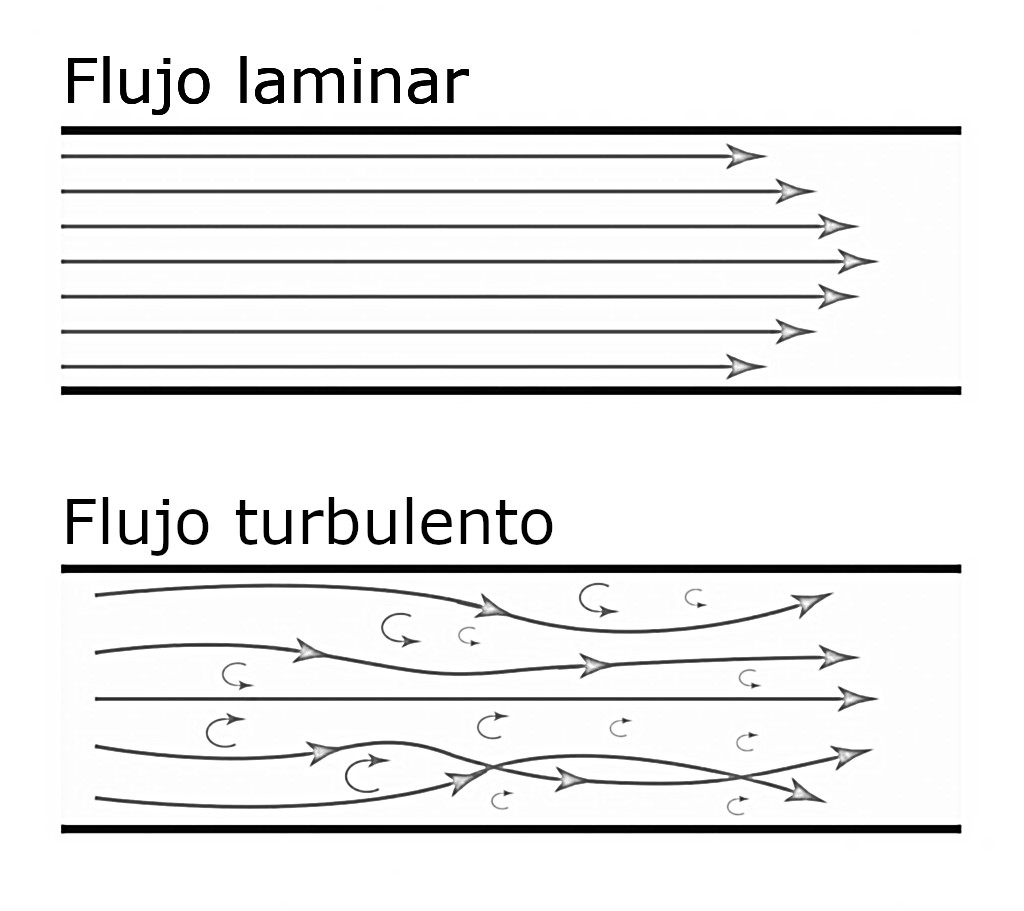
Untitled

La forma y el tamaño del objeto pueden contribuir a un flujo turbulento, por lo que pediremos un objeto pequeño en relación al volumen del fluido y de bordes redondeados, siendo una esfera la mejor de las opciones.

Fuerza viscosa

Cuando se propusieron las hipótesis de trabajo, se hablo de la velocidad del objeto en relación a su entorno. Ciertamente, la fuerza viscosa que se opone al movimiento del cuerpo está relacionado con la velocidad del cuerpo.

Si representamos a la fuerza viscosa mediante una función dependiente de la velocidad, $F_v(v)$ , podemos desarrollar una aproximación a la función mediante un polinomio de Taylor de grado dos evaluada en torno a una velocidad igual a cero. Esto es lo más lógico ya que las velocidades con las que trabajaremos son tendientes a cero, por lo que una buena aproximación puede ser encontrada en los puntos cercanos a las velocidad nula.

F_v(v) = F_v(v = 0) + F_v^\prime(v = 0)v + \frac{1}{2} F_v^{\prime \prime}(v = 0)v^2

Acorde a nuestras hipótesis, podemos decir que si la velocidad del cuerpo es nula, también lo es la magnitud de la fuerza viscosa: $F_v(v = 0) = 0$ .

Por otro lado, podemos limitar la velocidad del cuerpo a un punto en el que potencia al cuadrado sea despreciable o tendiente a cero. En ese caso $F_v^{\prime \prime}(v = 0)v^2 = 0$ .

Por último, definimos $F_v^\prime(v = 0) = b$ , siendo $b$ un coeficiente constante que llamaremos coeficiente de fuerza viscosa, quedando una ecuación con la siguiente forma

|\vec F_v| = b|\vec v|

A sabiendo de que la fuerza se opone al movimiento, podemos decir que

\vec F_v= -b\vec v

El coeficiente de fuerza viscosa es tan misterioso como los coeficientes de rozamiento, por lo que no se puede calcular. Solo se puede obtener de forma empírica.

Ecuación de movimiento en un fluido

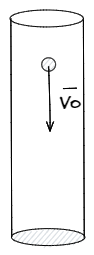
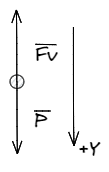
Untitled

Veamos el caso en el que un objeto cae en un fluido con una velocidad inicial. Aplicando las ecuaciones de Newton llegamos a:

\begin{split} P - F_v &= ma\\ mg - bv &= ma \end{split}

Para obtener la ecuación de la velocidad en función del tiempo, debemos resolver la ecuación diferencial

mg - bv = mv^\prime

Nuestra ecuación diferencial es lineal y de primer orden, por lo que podemos aplicar el factor integrante de Lagrange

Sea $v^\prime + \frac{b}{m}v = g$ la ecuación diferencial a resolver, con $p(t)=\frac{b}{m}$ y $q(t) = g$ . Definimos el factor de Lagrange como

\begin{split} u(t) &= e^{\int \frac{b}{m} dt }\\ u(t) &= e^{\frac{b}{m}(t-t_0) }\\ \end{split}

Si multiplicamos el facto en toda la ecuación diferencial obtenemos

\begin{split} u(t)v(t)^\prime + u(t)\frac{b}{m}v(t) &= u(t)g\\ (u(t)v(t))^\prime &= u(t)g \end{split}

Empecemos por integrar la primer parte de la ecuación que es mas sencillo

\begin{split} \int_{t_0}^t (u(t\prime)v(t\prime))^\prime dt &= u(t)v(t) - u(t_0)v(t_0)\\ &= u(t)v(t) - v(t_0)\\ &= u(t)v(t) - v_0 \end{split}

Pasemos a integrar la segunda parte de la ecuación

\begin{split} \int_{t_0}^t gu(t\prime) dt &= g \int_{t_0}^t u(t\prime) dt\\ &= g \int_{t_0}^t e^{\frac{b}{m}(t\prime-t_0) } dt \\ &= g \frac{m}{b}(e^{\frac{b}{m}(t\prime-t_0)})\bigg|^t_{t_0}\\ &= g \frac{m}{b}(e^{\frac{b}{m}(t-t_0)} - 1)\\ &= g \frac{m}{b}e^{\frac{b}{m}(t-t_0)} - g \frac{m}{b}\\ &= g \frac{m}{b}u(t) - g \frac{m}{b} \end{split}

Si juntamos ambas partes

\begin{split} u(t)v(t) - v_0 &= g \frac{m}{b}u(t) - g \frac{m}{b}\\ u(t)v(t) &= g \frac{m}{b}u(t) - g \frac{m}{b} + v_0\\ v(t) &= g \frac{m}{b} - g \frac{m}{b}\frac{1}{u(t)} + v_0\frac{1}{u(t)}\\ v(t) &= g \frac{m}{b} +(v_0 - g \frac{m}{b})\frac{1}{u(t)}\\ v(t) &= g \frac{m}{b} +(v_0 - g \frac{m}{b})e^{-\frac{b}{m}(t-t_0)} \end{split}

Para llegar a la ecuación de movimiento desde este punto es “fácil”. Simplemente hay que integrar

y(t) = g \frac{m}{b}(t-t_0) -(v_0 - g \frac{m}{b})\frac{m}{b}e^{-\frac{b}{m}(t-t_0)}

Velocidad limite

Observemos por un momento la ecuación de velocidad. ¿Qué ocurre si transcurre una cantidad infinita de tiempo?

v(t) = g \frac{m}{b} +(v_0 - g \frac{m}{b})e^{-\frac{b}{m}(t-t_0)}

Si transcurre una cantidad significativa tiempo, el coeficiente $e^{-\frac{b}{m}(t-t_0)}$ se aproximará a cero, haciendo que la velocidad tienda a $g \frac{m}{b}$ . A este valor se lo conoce como velocidad limite o terminal.

Otra forma de calcular la velocidad limite es a través de las ecuaciones de Newton.

mg - bv = ma

Cuando un cuerpo alcanza su velocidad limite en un medio viscoso, su peso y la fuerza viscosa se compensan, lo que implica que

mg - bv = 0

Entonces la velocidad limite $v_l$ es igual a

v_l = \frac{mg}{b}