profile photo

Guía 2 - Dinámica: Movimiento circular


hero image
Publicado el

Movimiento circular

Por lo que sabemos hasta ahora, cualquier cambio en la velocidad de un cuerpo se debe a la existencia de una aceleración. En el caso del movimiento circular uniforme, la velocidad se mantiene constante en tanto magnitud, pero no en cuanto a su dirección, y esto se debía a la existencia de una aceleración perpendicular al movimiento del cuerpo.

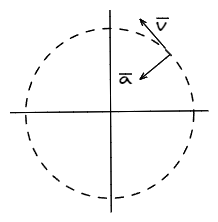
Untitled

Repasamos rápidamente las principales ecuaciones del movimiento circular. En coordenadas polares, se puede describir la posición, velocidad y aceleración de un cuerpo mediante las versores r^\hat r y θ^\hat \theta, como

r⃗(t)=rr^\vec r(t) = r\hat r
v⃗(t)=r˙r^+rθ˙θ^\vec v(t) = \dot r \hat r + r \dot \theta \hat \theta
a⃗(t)=(r¨−rθ˙2)r^+(rθ¨+2r˙θ˙)θ^\vec a(t) = (\ddot r - r {\dot \theta}^2 )\hat r + (r \ddot \theta + 2 \dot r \dot \theta)\hat \theta

Donde rr es la distancia entre el origen de coordenadas y el objeto en cuestión.

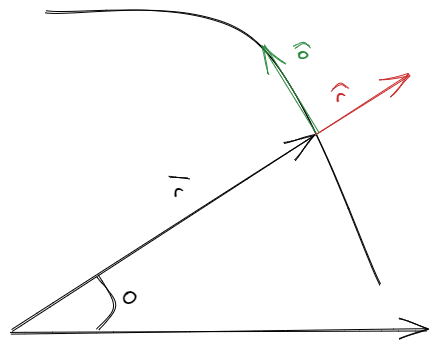
Untitled

Todo esto a sabiendas de que tanto θ^\hat \theta como r^\hat r acompañan al movimiento del cuerpo en todo instante de tiempo.

r^(t)=cos⁡θ(t)i^+sin⁡θ(t)j^\hat r(t) = \cos \theta(t) \hat i + \sin \theta(t) \hat j
θ^(t)=−sin⁡θ(t)i^+cos⁡θ(t)j^.\hat \theta (t) = -\sin\theta(t) \hat i + \cos \theta(t) \hat j.

En el caso en que el movimiento descripto por el cuerpo es circular de radio RR, entonces

r⃗(t)=Rr^\vec r(t)=R\hat r
v⃗(t)=Rθ˙θ^\vec v(t) = R\dot \theta \hat \theta
a⃗(t)=−Rθ˙2r^+Rθ¨θ^\vec a(t) = - R\dot \theta ^2 \hat r + R\ddot \theta \hat \theta

Donde θ˙\dot \theta se la describe como velocidad angular con la letra ω\omega y θ¨\ddot \theta como aceleración angular con la letra γ\gamma. Esto da paso a la ecuación para el movimiento angular de un cuerpo.

θ(t)=θ0+ω0t+12γt2\theta (t) = \theta_0 + \omega_0 t + \frac{1}{2} \gamma t^2
a⃗(t)=−Rω2r^+Rγθ^\vec a(t) = - R\omega ^2 \hat r + R\gamma\hat \theta
v⃗(t)=Rωθ^\vec v(t) = R\omega\hat \theta

Si el movimiento descripto por el cuerpo es circular y además uniforme, entonces tenemos un objeto recorre de forma periódica la misma trayectoria con la misma velocidad (en tanto magnitud), por ende, podemos hablar de periodo que es el tiempo en el que un objeto completa un giro.

Al periodo de un MCU se lo simboliza con la letra TT y se lo puede calcular a través de ω0=2πT\omega_0 = \frac{2 \pi}{T}.

Y si hablamos de periodo, podemos hablar de frecuencia, que se simboliza con la letra ν\nu y representa la cantidad de giros que realiza un objeto en una unidad de tiempo. Se lo puede calcular a través de TT como T=1νT = \frac{1}{\nu} o como ω0=2πν\omega_0 = 2\pi\nu.

Para MCU se simplifican aún más las ecuaciones de movimiento dadas, ya que γ=0\gamma = 0. Por tanto

a⃗(t)=−Rω02r^\vec a(t) = - R\omega_0 ^2 \hat r
v⃗(t)=Rω0θ^\vec v(t) = R\omega_0\hat \theta

La primera ecuación describe a la aceleración centrípeta, y la segunda a la velocidad tangencial. Cabe recalcar que para estos casos, la velocidad tangencial es constante en magnitud, es decir ∣v⃗∣=∣Rω0θ^∣=∣Rω0∣=Rω0=v|\vec v| = |R\omega_0\hat \theta| = |R\omega_0| = R\omega_0= v, por lo que se puede calcular la aceleración centrípeta como

a⃗(t)=−v2Rr^\vec a(t) = - \frac{v ^2}{R} \hat r

Esta aceleración es la responsable del movimiento de giro y su existencia es condición necesaria para el movimiento circular.

Fuerzas en el movimiento circular

Si un objeto realiza un movimiento circular, entonces debe existir una fuerza que provoque la aceración, a esta se la conoce como fuerza centrípeta. No se trata de una fuerza nueva, se puede dar por la tensión de una cuerda, por la atracción gravitatoria o por el contacto de vías. En definitiva, cualquier fuerza o resultante de fuerzas que apunten hacia el centro de giro será la fuerza centrípeta.

Veamos un caso particular. Analicemos un aspa del rotor de cola de un helicóptero largo RR, ¿Qué fuerzas actúan sobre el aspa? ¿Cómo actúan esas fuerzas con relación a los versores?

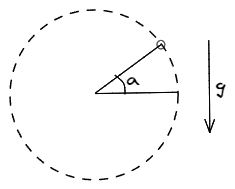
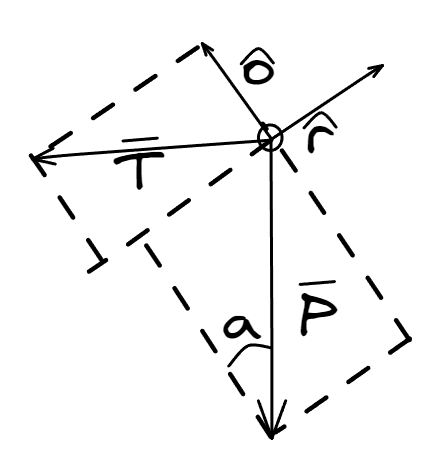
Untitled

Untitled

Sobre la dirección del versor r^\hat r actúan dos fuerzas, la fuerza de vinculo del aspa y el peso. Aplicando la segunda ley de Newton, la ecuación nos queda como

−Tr−Pr=−mRω2-T_r - P_r = -mR\omega^2

En la dirección del versor θ^\hat \theta también las mismas dos fuerzas. Aplicando la segunda ley de Newton, la ecuación nos queda como

Tθ−Pθ=mRγT_{\theta} - P_{\theta} = mR\gamma

Para que nuestro rotor de cola sea útil, es necesario que circule de forma sostenida a lo largo del tiempo, es decir que su velocidad angular sea constante. Con este datos, podemos decir que la fuerza TT que debe hacer el motor del rotor es igual a

Tr=mRω02−PrT_r = mR\omega_0^2 - P_r
Tθ=PθT_{\theta} = P_{\theta}