profile photo

Guía 1 - Movimiento circular, coordenadas polares, Movimiento relativo


hero image
Publicado el

Movimientos curvilíneos

Otra forma de expresar los vectores es en base a los versores de los ejes de coordenadas. Por ejemplo, si adoptamos los ejes cartesianos xx e yy, podemos expresar r⃗=(x,y)\vec r = (x, y) como r⃗=xi^+yj^\vec r = x \hat i + y \hat j donde i^\hat i y j^\hat j son los versores de los ejes xx e yy.

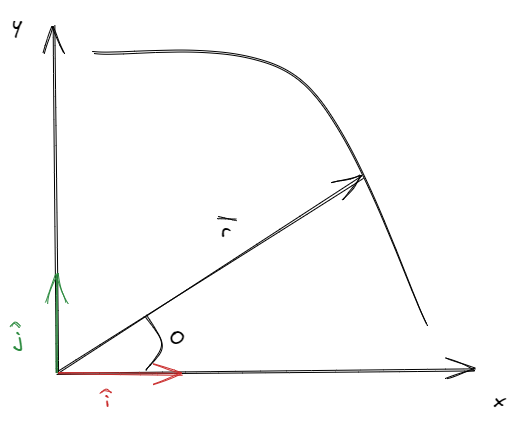
Untitled

Una forma alternativa de describir vectores es utilizando coordenadas polares. En este sistema, un vector r⃗\vec{r} se describe mediante su magnitud r=∣r⃗∣r = |\vec r| y su ángulo θ\theta respecto a un eje de referencia que en general es el eje xx. Las coordenadas polares se pueden expresar como r⃗=rr^\vec{r} = r\hat{r}, donde r^\hat{r} es un versor unitario que apunta en la dirección del vector.

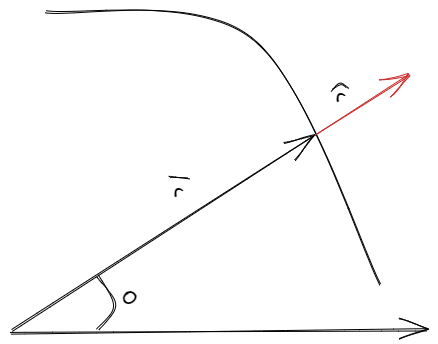
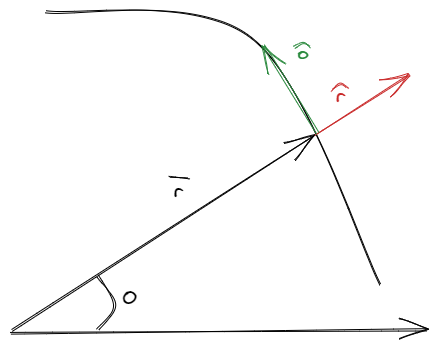
Untitled

Untitled

Cuando uno observa la nueva notación r⃗=rr^\vec{r} = r\hat{r}, puede preguntarse donde se encuentra expresado θ\theta. Este último valor esta implícito dentro del verso r^\hat r. En la modida que r^\hat r cambia, θ\theta tambíen lo hace. Esto no ocuerre con las coordenadas cartesianas, donde las componentes son totalmente independientes.

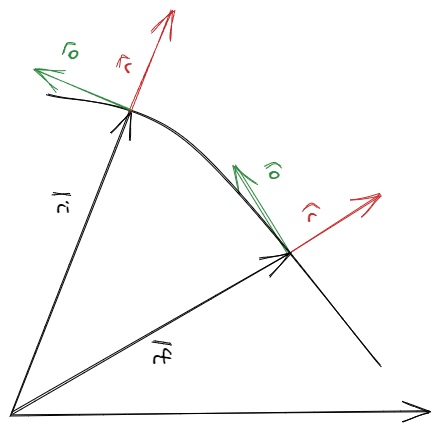
Untitled

Otra dificultad con la que nos vamos a encontrar es al momento de derivar r⃗\vec r. En coordenadas cartesianas, derivar era algo sencillo ya que se trataba de una suma:

r⃗(t)=x(t)i^+y(t)j^\vec r(t) = x(t) \hat i + y(t) \hat j
r⃗(t)˙=x(t)˙i^+y(t)˙j^\dot{\vec r(t)} = \dot{x(t)} \hat i + \dot{y(t)} \hat j

Dado que i^\hat i y j^\hat j son constantes, todo quedaba en derivar x(t)x(t) e y(t)y(t), pero en coordenadas polares debemos derivar un producto y una función compuesta

r⃗(t)=r(t)r^(t)\vec{r}(t) = r(t)\hat r(t)

Donde r^(t)\hat r(t) lo podemos expresar en coordenadas cartesianas como:

r^(t)=cos⁡θ(t)i^+sin⁡θ(t)j^\hat r(t) = \cos \theta(t) \hat i + \sin \theta(t) \hat j

Entonces para obtener la velocidad en coordenadas polares

v⃗=r⃗˙=(rr^)˙=r˙r^+rr^˙\vec v = \dot{\vec r} = \dot{(r \hat r)} = \dot r \hat r + r \dot{\hat r}

Ahora debemos saber como derivar r^˙\dot{\hat r}. Para esto hay que tener en cuenta que:

r^˙=(cos⁡θi^+sin⁡θj^)˙=(cos⁡θi^)˙+(sin⁡θj^)˙\dot{\hat r} = \dot{(\cos \theta \hat i + \sin \theta \hat j)} = \dot{(\cos \theta \hat i)} + \dot{(\sin \theta \hat j)}

Y por tanto (recordar la regla de la cadena)

r^˙=−θ˙sin⁡θi^+θ˙cos⁡θj^=θ˙θ^\dot{\hat r} = - \dot \theta \sin \theta \hat i + \dot \theta \cos \theta \hat j = \dot \theta \hat \theta

Entonces, la velocidad queda expresada como

v⃗=r˙r^+rθ˙θ^\vec v = \dot r \hat r + r \dot \theta \hat \theta

Se puede decir que r˙r^\dot r \hat r representa la velocidad radial, mientras que rθ˙θ^r\dot \theta \hat \theta representa la velocidad “en θ\theta”.

El siguiente paso es obtener a⃗\vec a como la derivada de la velocidad. Para llevar adelante esta engorrosa tarea, antes vamos a calcular la derivada de θ^\hat \theta

θ^˙=(−sin⁡θi^)˙+(cos⁡θj^)˙=−θ˙cos⁡θi^−θ˙sin⁡θj^=−θ˙r^\begin{split} \dot{\hat\theta} &= \dot{(-\sin\theta\hat i)} + \dot{(\cos \theta \hat j)} \\ &=-\dot \theta \cos \theta \hat i - \dot \theta \sin \theta \hat j\\ &= -\dot \theta \hat r \end{split}

Con este resultado, tratamos de llegar a la expresión de la aceleración

a⃗=v⃗˙=r¨r^+r˙r^˙+(rθ˙)˙θ^+(rθ˙)θ^˙=r¨r^+r˙r^˙+(r˙θ˙+rθ¨)θ^+(rθ˙)θ^˙=r¨r^+r˙θ˙θ^+(r˙θ˙+rθ¨)θ^−(rθ˙)θ˙r^=r¨r^+r˙θ˙θ^+(r˙θ˙+rθ¨)θ^−rθ˙2r^a⃗=(r¨−rθ˙2)r^+(rθ¨+2r˙θ˙)θ^\begin{split} \vec a = \dot{\vec v} &= \ddot r \hat r + \dot r \dot{\hat r} + \dot{(r\dot \theta)}\hat \theta + (r\dot\theta)\dot{\hat\theta} \\ &= \ddot r \hat r + \dot r \dot{\hat r} + (\dot r\dot\theta + r\ddot\theta)\hat\theta + (r\dot\theta)\dot{\hat\theta}\\ &= \ddot r \hat r + \dot r \dot\theta\hat\theta + (\dot r\dot\theta + r\ddot\theta)\hat\theta - (r\dot\theta)\dot\theta\hat r\\ &= \ddot r \hat r + \dot r \dot\theta\hat\theta + (\dot r\dot\theta + r\ddot\theta)\hat\theta - r\dot\theta^2\hat r\\ \vec a &= (\ddot r - r {\dot \theta}^2 )\hat r + (r \ddot \theta + 2 \dot r \dot \theta)\hat \theta \end{split}

Donde (r¨−rθ˙2)r^(\ddot r - r {\dot \theta}^2 )\hat r es conocida como la aceleración radial o centrípeta, mientras que (rθ¨+2r˙θ˙)θ^(r \ddot \theta + 2 \dot r \dot \theta)\hat \theta es la aceleración en θ\theta

Movimiento circular

Describir movimientos del tipo rectilíneos u oblicuos mediante coordenadas polares no tiene sentido en si mismo debido a su complejidad en comparación a las coordenadas cartesianas. Sin embargo, cuando el movimiento a describir es del tipo circular, la complejidad se invierte.

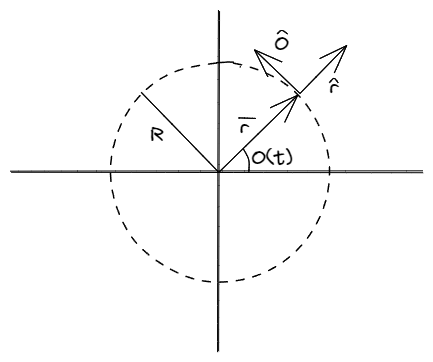
Untitled

Si un móvil describe un movimiento circular de radio RR constante, entonces r⃗(t)=R\vec r (t) = R es constante para todo tt y lo único que varia es θ(t)\theta (t). Hasta ahora no le prestamos mucha atención a la variación del ángulo, pero ahora tiene sentido derivarla y obtener ω=θ˙(t)\omega = \dot \theta (t) que se conoce como velocidad angular.

En cuanto a las unidades, se suele usar radiantes para θ\theta dado que si los multiplicamos por el radio del movimiento, obtenemos el arco recorrido. Dicho lo anterior, decimos que [ω]=rads[\omega] = \frac{rad}{s} aunque es muy común obviar los radrad y expresar sus unidades como [ω]=1s[\omega] = \frac{1}{s}.

Siguiendo nuestra línea de trabajo, no tardamos en llegar al concepto de aceleración angular definida como γ=ω˙=θ¨\gamma = \dot \omega = \ddot \theta, donde [γ]=1s2[\gamma] = \frac{1}{s^2}.

Análogamente a lo que ya vimos, podemos definir las ecuaciones de movimiento angular como

θ(t)=θ0+ω0t+12γt2\theta (t) = \theta_0 + \omega_0 t + \frac{1}{2} \gamma t^2
ω(t)=ω0+γt\omega (t) = \omega_0 + \gamma t

Dado que ∣r⃗∣=r=R|\vec r| = r = R es constante para todo instante de tiempo tt, simplifica bastante las ecuaciones antes dadas para aceleración y velocidad, quedando

v⃗=Rωθ^\vec v = R\omega \hat \theta

Notar que la velocidad esta definido únicamente sobre el versor θ^\hat \theta que es tangente al movimiento, razón por la cual, a esta velocidad se la llama velocidad tangencial.

a⃗=−Rω2r^+Rγθ^\vec a = -R\omega^2 \hat r + R \gamma \hat \theta

En este caso, la aceleración posee componentes tanto en r^\hat r versor como en θ^\hat \theta versor. A la componente en θ^\hat \theta se la conoce como aceleración tangencial.

Observar que la componente en r^\hat r que llamamos aceleración centrípeta, es negativa, es decir, apunta hacia el centro del movimiento circular. Esta aceleración es la responsable del movimiento circular. De hecho, podemos tener una aceleración tangencial nula y aun poseer un movimiento circular. A este caso se lo conoce como movimiento circular uniforme (MCU) donde γ=0\gamma = 0 y el modulo de la velocidad tangencial es siempre constante, es decir, ω=ω0\omega = \omega_0, y la aceleración centrípeta también resulta constante a⃗=−Rωo2r^\vec a = -R {\omega_o}^2 \hat r .

En MCU tenemos que un objeto recorre de forma periódica la misma trayectoria con la misma velocidad (en tanto magnitud), por ende, podemos hablar de periodo que es el tiempo en el que un objeto completa un giro.

Al periodo de un MCU se lo simboliza con la letra TT y se lo puede calcular a través de ω0=2πT\omega_0 = \frac{2 \pi}{T}.

Y si hablamos de periodo, podemos hablar de frecuencia, que se simboliza con la letra ν\nu y representa la cantidad de giros que realiza un objeto en una unidad de tiempo. Se lo puede calcular a través de TT como T=1νT = \frac{1}{\nu} o como ω0=2πν\omega_0 = 2\pi\nu.

Movimiento relativo

Dado dos observadores oo y o′o\prime, con sus propios sistemas de referencia, pueden observar a un mismo objeto y describirlo de forma distinta.

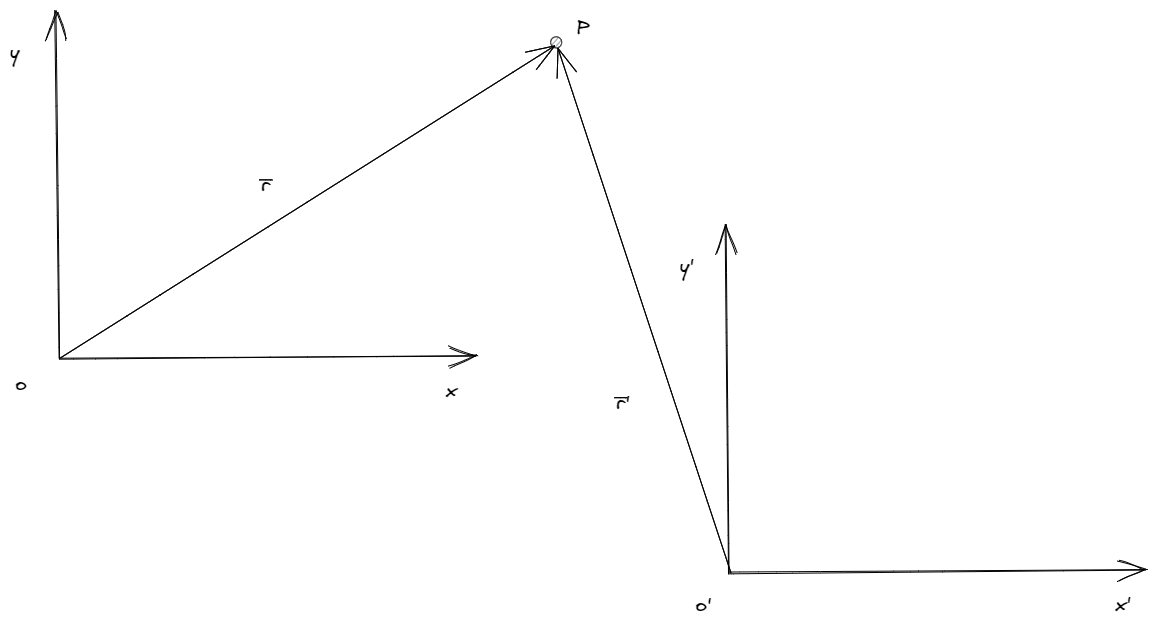
Untitled

En estos casos, lo que se suele plantear es a un observador como fijo, digamos oo (esto por convención) y a través de él describir al sistema de referencia de o′o\prime.

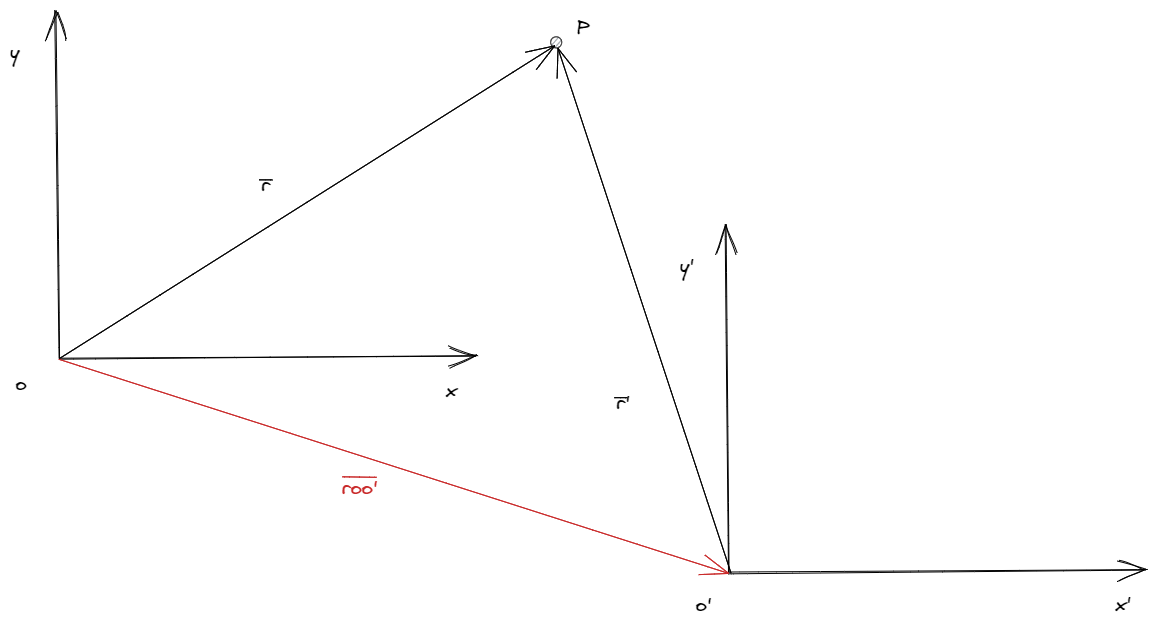
Untitled

De esta forma, podemos establecer una relación entre los observadores y el objeto observado

r⃗=r⃗′+r⃗00′\vec r = \vec r \prime + \vec r_{0 0\prime}

Con esto, ya podemos determinar las subsecuentes magnitudes: velocidad y aceleración

v⃗=r⃗˙=r⃗˙′+r⃗oo′˙=v⃗′+v⃗oo′\vec v = \dot{\vec r} = \dot{\vec r} \prime + \dot{\vec r_{oo \prime}} = \vec v \prime + \vec v_{oo\prime}
a⃗=v⃗˙=v⃗˙′+v⃗oo′˙=a⃗′+a⃗oo′\vec a = \dot{\vec v} = \dot{\vec v} \prime + \dot{\vec v_{oo \prime}} = \vec a \prime + \vec a_{oo\prime}