profile photo

Guía 1 - Cinemática: velocidad, aceleración, MRU, MRUV


hero image
Publicado el

Análisis dimensional

El análisis dimensional nos permite verificar la consistencia de las ecuaciones que describen el movimiento de un objeto. También nos permite identificar las unidades de medida de las variables que intervienen en las ecuaciones y expresar las soluciones en unidades apropiadas. Por ejemplo, si tenemos una ecuación que describe la velocidad de un objeto en términos de su posición y tiempo, el análisis dimensional nos permitiría verificar que la ecuación tiene unidades de longitud dividido por tiempo, lo que corresponde a unidades de velocidad.

Incertidumbre

En física, la incertidumbre se refiere a la falta de precisión en una medición. Las mediciones siempre tienen cierto grado de incertidumbre debido a factores como la precisión del instrumento de medición, la habilidad del observador y el ruido en los datos. Se puede expresar la incertidumbre en términos de desviación estándar o error estándar, y se utiliza para estimar la precisión de los resultados experimentales. Es importante tener en cuenta la incertidumbre al interpretar los resultados y al hacer comparaciones entre mediciones.

Ordenes de magnitud

Cuando hablamos de órdenes de magnitud, nos referimos a la escala numérica de una cantidad. Por ejemplo, si decimos que una masa es del orden de magnitud de 10310^3 kilogramos, eso significa que la masa está en el rango de miles de kilogramos. Los órdenes de magnitud se utilizan a menudo para hacer aproximaciones rápidas y para comparar magnitudes de diferentes escalas. Por ejemplo, la masa de una persona es del orden de magnitud de 10210^2 kilogramos, mientras que la masa de un automóvil es del orden de magnitud de 10310^3 kilogramos.

Sistema de referencia

Un sistema de referencia es un conjunto de coordenadas que se utiliza para describir la posición y el movimiento de un objeto. Se puede elegir cualquier punto del espacio como origen y establecer ejes de coordenadas para describir la posición del objeto en función del tiempo. El sistema de referencia elegido debe ser inercial, lo que significa que no debe estar acelerando en relación con un marco de referencia absoluto.

La trayectoria de un objeto es el camino que sigue a lo largo del tiempo. Se puede describir en términos de distancia y dirección en un sistema de coordenadas. En la cinemática, se utiliza la trayectoria para calcular la velocidad y la aceleración del objeto.

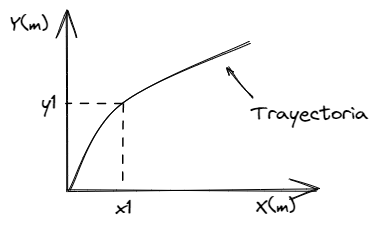
En este grafico, describimos la trayectoria de un objeto en un sistema de coordenadas bidimensional.

En este grafico, describimos la trayectoria de un objeto en un sistema de coordenadas bidimensional.

Posición en función del tiempo

El grafico de posición en función del tiempo es una herramienta muy útil para visualizar la trayectoria de un objeto. En este tipo de gráfico, la posición del objeto se representa en el eje vertical y el tiempo en el eje horizontal. Al trazar la posición del objeto en diferentes momentos, se puede ver cómo cambia su posición en el tiempo y determinar su velocidad y aceleración.

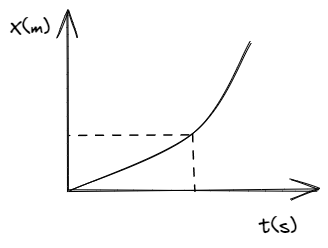
Para función que describe la trayectoria de un cuerpo en función del tiempo suele tener la notación x(t).

Para función que describe la trayectoria de un cuerpo en función del tiempo suele tener la notación x(t)x(t).

Si el movimiento es unidimensional, con un grafico como el que acabamos de describir es más que suficiente, pero si el movimiento es bidimensional o tridimensional, usaremos más de un grafico para describir la trayectoria del cuerpo en función del tiempo.

Movimiento unidimensional o cinemática en una dimensión

El movimiento unidimensional se refiere a aquel en el que un objeto se mueve en una sola dirección, es decir, a lo largo de una sola dimensión.

Un sistema de referencia para un movimiento unidimensional puede ser una recta.

Un sistema de referencia para un movimiento unidimensional puede ser una recta.

Un simplificación que realizaremos para el estudio de la cinemática en una dimensión es tomar el cuerpo de estudio para un objeto puntual.

Desplazamiento

El desplazamiento es una magnitud vectorial que representa la distancia y la dirección entre el punto de partida y el punto final de un objeto en movimiento. Se puede calcular restando la posición final del objeto de su posición inicial. El desplazamiento se expresa en metros (m) en el Sistema Internacional de Unidades (SI), y su dirección se indica con un vector unitario. El sentido del desplazamiento se puede determinar mediante la comparación de la posición inicial y final del objeto.

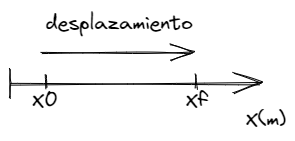
Untitled

La diferencia entre magnitudes vectoriales y escalares radica en la información que brindan. Las magnitudes escalares solo indican una cantidad numérica, mientras que las magnitudes vectoriales también incluyen información sobre la dirección y el sentido del vector. Por ejemplo, la masa es una magnitud escalar, mientras que la velocidad es una magnitud vectorial ya que incluye información sobre la dirección y el sentido en que se mueve el objeto.

Podemos decir que el desplazamiento es un vector porque posee magnitud, dirección y sentido, pero además, por estar definido como la resta entre dos vectores como lo son xf⃗\vec{x_f} y xo⃗\vec{x_o}.

Δx⃗=xf⃗−xo⃗\Delta \vec{x} = \vec{x_f} - \vec{x_o}

Velocidad media

Para conocer este concepto y conectarlo con la sección anterior veamos un ejemplo.

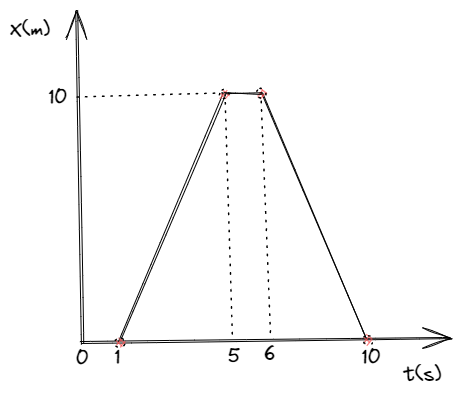
Untitled

Dado un cuerpo puntual en movimiento, se determina su posición para cuatro instantes distintos de tiempo. Se desconoce totalmente la posición del objeto en instantes intermedios de tiempo. A pesar de estas limitaciones, podemos extraer información haciendo uso del concepto de velocidad media.

Decimos que la velocidad media de un objeto es la razón entre la distancia recorrida y el tiempo transcurrido. Se puede calcular mediante la siguiente fórmula:

v⃗media=Δx⃗Δt\vec{v}_{media} = \frac{\Delta \vec{x}}{\Delta t}

La velocidad media es el resultado del producto entre un escalar y un vector 1ΔtΔx⃗\frac{1}{\Delta t} \Delta \vec{x} por lo que también es un vector.

Volviendo a nuestro ejemplo, podemos decir que la velocidad media entre los instantes uno y cinco es:

v⃗1−5=Δx⃗Δt=10m−0m5s−1s=2,5ms\begin{split} \vec{v}_{1-5} = \frac{\Delta \vec{x}}{\Delta t} = \frac{10m - 0m}{5s - 1s} = 2,5 \frac{m}{s} \end{split}

Entro los instantes cinco y seis es cero, y entre los instantes seis y diez es:

v⃗6−10=Δx⃗Δt=0m−10m10s−6s=−2,5ms\vec{v}_{6-10} = \frac{\Delta \vec{x}}{\Delta t} = \frac{0m - 10m}{10s - 6s} = -2,5 \frac{m}{s}

Aquí vemos el carácter vectorial de la velocidad media mediante el signo de las magnitudes, indicando que el objeto invierte su sentido en el ultimo tercio de su recorrido con relación al primero.

Notar que v⃗1−5\vec v_{1-5} es la velocidad a la cual debería ir el objeto para recorrer esa distancia en ese lapso de tiempo. Esto podría no ser así. El objeto podría no desplazarse durante los primeros tres segundos, y acelerar en solo un segundo para alcanzar los diez metros finales.

Si calculamos la velocidad media para el lapso entre uno y diez segundos, el resultado seria cero. ¿Significa esto que el objeto se quedo quieto? Claramente no.

Esto nos muestra lo limitado que es la vmediav_{media}, pero es un excelente punta pie para una definición más general de lo que es la velocidad.

Velocidad instantánea

La velocidad instantánea es la velocidad de un objeto en un momento particular del tiempo. Se puede calcular encontrando la derivada de la posición del objeto en función del tiempo. En otras palabras, la velocidad instantánea es la tangente a la curva de posición en un punto específico. La velocidad instantánea se expresa en metros por segundo (m/s) en el Sistema Internacional de Unidades (SI).

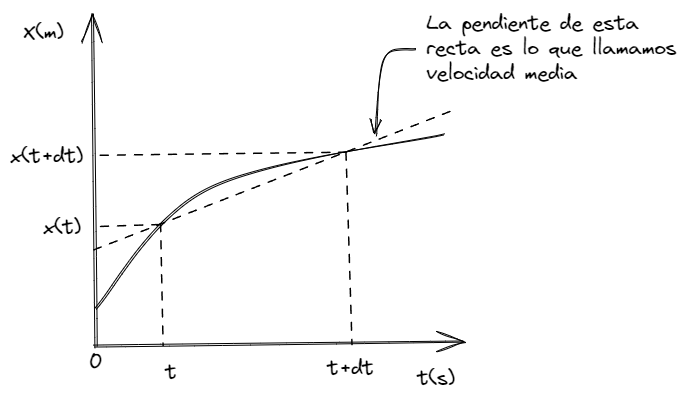
Untitled

Dado x(t)x(t) podemos definir a la velocidad media como:

vm(t)=x(t+Δt)−x(t)Δtv_m(t) = \frac{x(t + \Delta t) - x(t)}{\Delta t}

Y a la velocidad instantánea como

vi(t)=lim⁡Δt→0vm(t)=lim⁡Δt→0x(t+Δt)−x(t)Δt\begin{split} v_i(t) &= \lim_{\Delta t \rightarrow 0} v_m(t)\\ &= \lim_{\Delta t \rightarrow 0} \frac{x(t + \Delta t) - x(t)}{\Delta t} \end{split}

Y esto no es otra cosa más que x′(t)x'(t) o dxdt\frac{dx}{dt} o x˙(t)\dot x(t).

v⃗=x⃗˙(t)\vec{v} = \dot{ \vec{x}}(t)

No perder de vista que la velocidad es un vector.

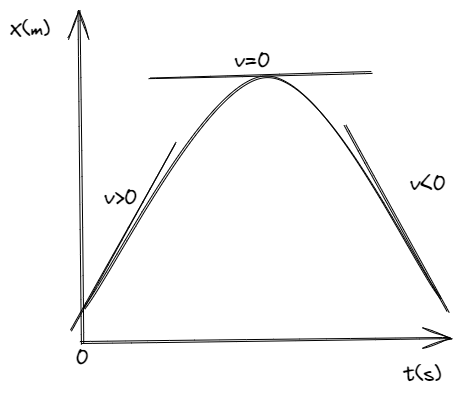
Untitled

Aceleración

Para llegar al concepto de aceleración partiremos, al igual que con la velocidad, de la aceleración media

a⃗media=Δv⃗Δt\vec a_{media} = \frac{\Delta \vec v}{\Delta t}

Su relación con la velocidad dependerá del sistema de referencia. Esto quiere decir que ∣v⃗∣|\vec v| aumentara o disminuirá, dependiendo de si los vectores v⃗m\vec v_m y a⃗m\vec a_m comparte o no, la misma dirección y sentido.

De la misma forma que antes, podemos definir una aceleración instantánea como

a⃗(t)=lim⁡Δt→0Δv⃗Δt=lim⁡Δt→0v(t+Δt)−v(t)Δt=v˙(t)=x¨(t)\begin{split} \vec a(t) &= \lim_{\Delta t \rightarrow 0} \frac{\Delta \vec v}{\Delta t}\\ &= \lim_{\Delta t \rightarrow 0} \frac{v(t + \Delta t) - v(t)}{\Delta t}\\ &= \dot v(t)\\ &= \ddot x(t) \end{split}

Graficas para ejemplificar

Si la posición del objeto es constante para todo instante de tiempo, quiere decir que se encuentra inmóvil, y por tanto su velocidad es nula, al igual que su aceleración.

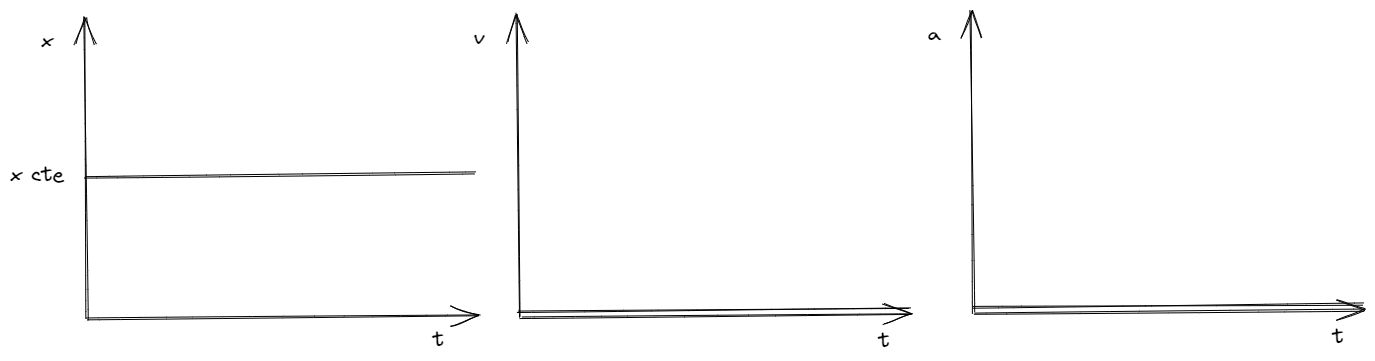
Untitled

Por otro lado, si la velocidad del objeto es constante y positiva, entonces, su aceleración es nula y su posición varia de forma constante.

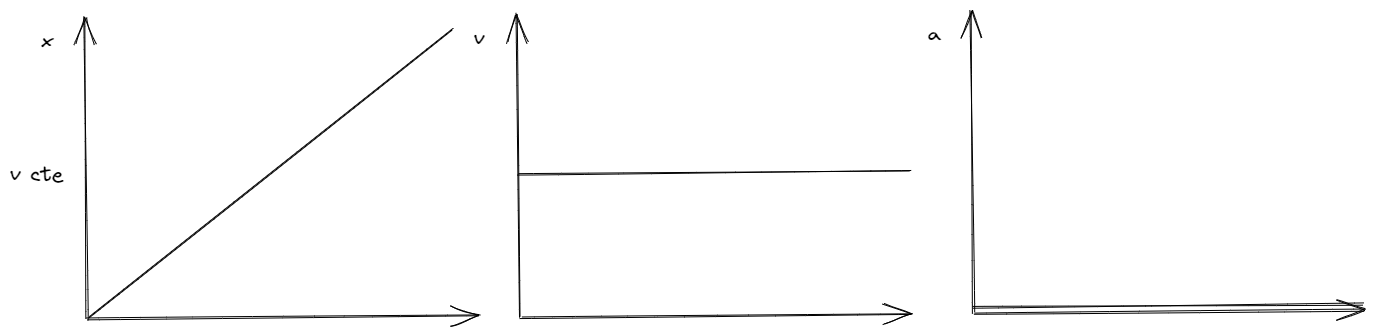
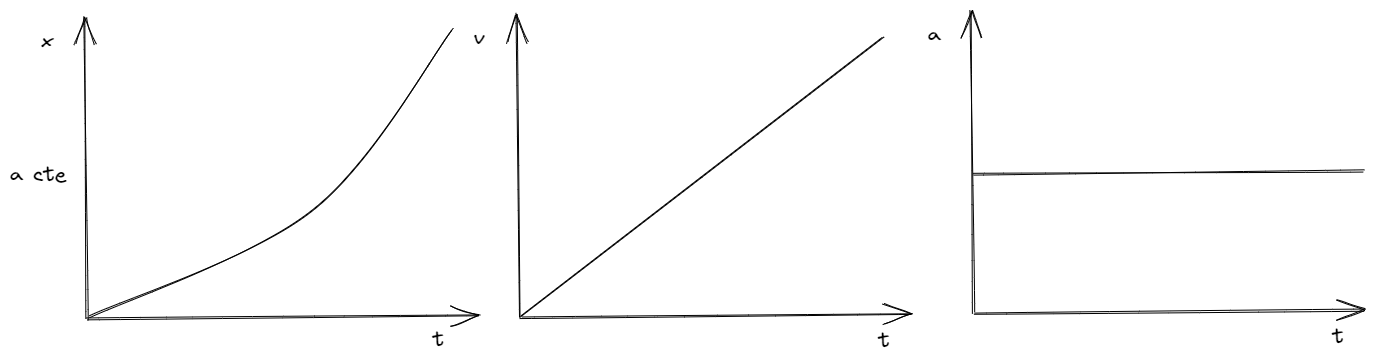
Untitled

Por último, si la aceleración es constante y positiva, entonces, la velocidad del objeto va a crecer de forma lineal y su posición varia de acuerdo a una función cuadrática.

Untitled

Ecuaciones de movimiento

Las ecuaciones de movimiento para un objeto en movimiento rectilíneo uniformemente acelerado (MRUA) son:

a⃗(t)=a⃗0\vec a(t) = \vec a_0

Dado que la aceleración es constante para todo instante de tiempo, podemos decir que:

a⃗0=v⃗(t)−v⃗(t0)t−t0\vec a_0 = \frac{\vec v(t) - \vec v(t_0)}{t - t_0}

Por tanto, la velocidad en cada instante de tiempo es:

v⃗(t)=v⃗(t0)+a⃗0(t−t0)\vec v(t) = \vec v(t_0) + \vec a_0(t - t_0)

Observar que se trata de una recta y que es coherente con las graficas antes vistas

Untitled

Dado que la velocidad no es constante, no podemos forzar la ecuación de posición en función del tiempo de la misma forma que lo hicimos con la velocidad. Pero como la velocidad v⃗(t)\vec v(t) es una recta, siempre vale que la velocidad media es el promedio aritmético entre v⃗(t)\vec v(t) y la velocidad inicial v⃗(t0)=v⃗0\vec v(t_0) = \vec v_0. Es decir que, en este caso en particular, la velocidad media es

v⃗m=v⃗(t)+v⃗02\vec v_m = \frac{\vec v(t) + \vec v_0}{2}

Por otro lado sabemos que

v⃗m=x⃗(t)−x⃗(t0)t−t0\vec v_m =\frac{\vec x(t) - \vec x(t_0)}{t-t_0}

Y por lo mencionado anteriormente

v⃗m=x⃗(t)−x⃗(t0)t−t0=v⃗(t)+v⃗02\vec v_m =\frac{\vec x(t) - \vec x(t_0)}{t-t_0} = \frac{\vec v(t) + \vec v_0}{2}

Entonces

x⃗(t)−x⃗(t0)t−t0=v⃗(t)+v⃗02\frac{\vec x(t) - \vec x(t_0)}{t-t_0} = \frac{\vec v(t) + \vec v_0}{2}

Despejando x⃗(t)\vec x(t) llegamos a

x⃗(t)=x⃗(t0)+12(v⃗(t)+v⃗0)(t−t0)\vec x(t) = \vec x(t_0) + \frac{1}{2}(\vec v(t) + \vec v_0)(t-t_0)

Reemplazando v⃗(t)\vec v(t) por v⃗0+a⃗0(t−t0)\vec v_0 + \vec a_0(t - t_0)

x⃗(t)=x⃗(t0)+v⃗0(t−t0)+12a⃗0(t−t0)2\vec x(t) = \vec x(t_0) + \vec v_0(t-t_0) + \frac{1}{2} \vec a_0(t-t_0)^2

Notar que si a⃗0=0\vec a_0 = 0 entonces encontramos las ecuaciones para un movimiento rectilíneo uniforme (MRU)

x⃗(t)=x⃗(t0)+v⃗0(t−t0)\vec x(t) = \vec x(t_0) + \vec v_0(t-t_0)
v⃗(t)=v⃗(t0)\vec v(t) = \vec v(t_0)

Ahora, si tomamos en cuenta las ecuaciones de velocidad y aceleración del MRUA

v⃗(t)=v⃗(t0)+a⃗0(t−t0)\vec v(t) = \vec v(t_0) + \vec a_0(t - t_0)
x⃗(t)=x⃗(t0)+v⃗0(t−t0)+12a⃗0(t−t0)2\vec x(t) = \vec x(t_0) + \vec v_0(t-t_0) + \frac{1}{2} \vec a_0(t-t_0)^2

Si despejamos (t−t0)(t - t_0) de la ecuación de velocidad

(t−t0)=v⃗(t)−v⃗(t0)a⃗0(t - t_0) = \frac{\vec v(t) - \vec v(t_0) }{\vec a_0}

Y lo reemplazamos en la ecuación de aceleración

x⃗(t)=x⃗(t0)+v⃗0v⃗(t)−v⃗(t0)a⃗0+12a⃗0v⃗(t)−v⃗(t0)a⃗02\begin{split} \vec x(t) &= \vec x(t_0) \\ &+ \vec v_0\frac{\vec v(t) - \vec v(t_0) }{\vec a_0} \\ &+ \frac{1}{2} \vec a_0\frac{\vec v(t) - \vec v(t_0) }{\vec a_0}^2 \end{split}

Podemos llegar a la siguiente ecuación que puede resultarnos de ayuda

v⃗(t)2=v⃗(to)2+2a⃗0(x⃗(t)−x⃗(t0))\vec v(t) ^2 = \vec v(t_o) ^2 + 2 \vec a_0(\vec x(t) - \vec x(t_0))

Los ejemplos clásicos para este tipo de ecuaciones son el tiro vertical y caída libre.