Guía 7 - Interacción gravitatoria

Publicado el 6/21/2023

Potencial gravitatorio

Se define el potencial gravitatorio como la cantidad de trabajo que se debe realizar para mover una masa puntual desde un punto de referencia a un punto específico en el campo gravitatorio. Este potencial se puede calcular utilizando la ley de gravitación universal de Newton y se puede expresar en términos de la masa de los objetos y la distancia entre ellos.

V(r) = - \frac{GMm}{r}

Donde $G$ es la constante gravitatoria, $M$ y $m$ son las masas de los objetos, $r$ es la distancia entre ellos. Cuanto mayor sea dicha distancia, más pequeño se hace el potencial (lo la fuerza de atracción si así se desea pensar), hasta llegar a cero, donde alcanza su máximo valor, razón por la cual, siempre será negativo.

Para calcular el potencial gravitatorio en un punto específico, se necesita saber la posición y la masa de todas las partículas que generan el campo gravitatorio en ese punto. Una vez que se conoce esto, se puede utilizar la ley de gravitación universal para calcular el potencial gravitatorio en ese punto.

El potencial gravitatorio es una cantidad escalar y se puede utilizar para calcular la energía potencial gravitatoria.

En relación al diagrama de energía del potencial gravitatorio, podemos divisar tres casos interesantes para pensar. El primero de ellos es pensar el potencial y su relación con una energía mecánica mayor a cero.

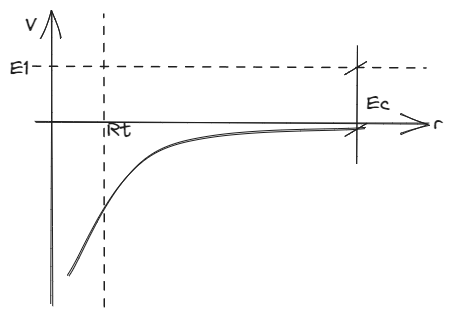
Untitled

En el diagrama podemos ver las siglas $Rt$ que hacen referencia al radio terrestre. Esta funciona como una cota de mínima para los valores que puede adoptar $r$ , dado que las distancia entre los cuerpos de estudio no puede ser menor al radio de la tierra.

Si la energía disponible es mayor a cero, entonces se tiene el potencial de alcanzar el infinito sin ningún problema. Es mas, podemos alcanzar el infinito y con energía cinética de sobra.

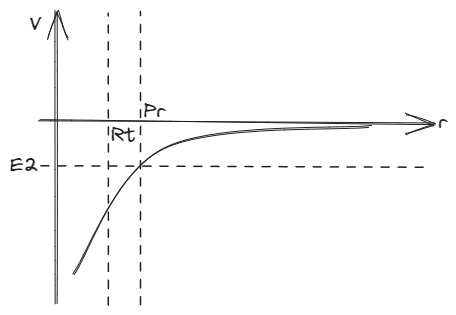
Untitled

Si por otro lado, la energía disponible es menor a cero, entonces nos encontraríamos con un punto de retorno.

El último de los casos es aquel en el que la energía es igual a cero. En este caso, el infinito es igual de alcanzable que en el primero de los ejemplos, pero la energía cinética se reduciría casi a cero. Esta conclusión nos indica que si uno quisiera escapar de la tierra, necesita como mínimo una energía igual a cero.

\begin{split} E&=0\\ E_c + E_p &= 0\\ \frac{1}{2}mv_e^2 - \frac{GM_tm}{R_t} &= 0\\ v_e &= (\frac{2GM_t}{R_t})^{\frac{1}{2}} \end{split}

Este último resultado nos indica cual debiera ser la velocidad de escape ( $v_e$ ) para abandonar la tierra, siendo $R_t, M_t$ el radio y la masa terrestre.

Comentario final, se puede observar como la velocidad de escape no depende del proyectil (o de lo que sea que se quiera enviar al espacio).

Interacción gravitatoria

La ley de gravitación universal propone que dado dos objetos de masa $m_1, m_2$ , ambas percibirán fuerzas de atracción en dirección de la recta que las une, de igual magnitud, pero de sentido contrario.

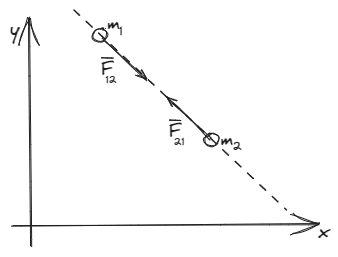
Untitled

Dicha fuerza será proporcional a sus masa pero inversamente proporcionales a la distancia que las separa.

\vec F_{12} = \frac{Gm_1m_2}{r_{12}^2} \hat r_{12} = -\vec F_{21}

La constante $G$ o constante de gravitación tiene un valor aproximado de $6,672\times 10^{-11}\frac{m^3}{kg \cdot seg^2}$ . El símbolo $r_{12}$ representa la distancia entre los cuerpos, mientras que el versor $\hat r_{12}$ , es un versor que se encuentra sobre la recta que contiene a los cuerpos y apunta en el sentido $m_1\rightarrow m_2$ .

En una versión aún más general, la ley se puede representar en tanto la posición relativa de los cuerpos

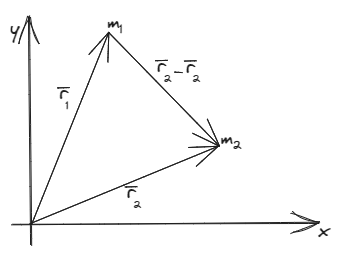
Untitled

\vec F_{12} = \frac{Gm_1m_2}{|\vec r_2-\vec r_1|^3} (\vec r_2-\vec r_1) = -\vec F_{21}

En esta representación se aplica el intercambio $\hat r_{12} = \frac{\vec r_2-\vec r_1}{|\vec r_2-\vec r_1|}$ , razón por la cual vemos un denominador al cubo. Por nomenclatura, nos referimos a $m_1$ como masa fuente, mientras que a $m_2$ lo identificaremos como masa campo. Es decir, nos encontramos con la fuente del campo gravitatorio y el punto donde se evalúa dicho campo.

Proyectil en orbita circular

Supongamos que se desea poner en orbita a un satélite de masa $m$ . Dicha tarea requiere entre muchas otras cosas, conocer la velocidad necesaria para que el mencionado cuerpo realice un movimiento circular uniforme alrededor de la tierra y a una distancia $r$ del centro del planeta.

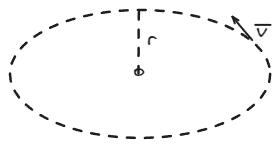
Untitled

Para lograr un MCU, es necesario que la fuerza gravitatoria sea igual al producto de la masa por la aceleración centrípeta.

\begin{split} \vec F_G = m \cdot a_c\\ \end{split}

Por ser un MCU, la aceleración centrípeta es $a_c = -\frac{v^2}{r}$ , siendo $v$ la velocidad tangencial constante, desconocida por el momento, necesaria para poner en orbita el satélite.

\begin{split} \vec F_G &= m \cdot a_c\\ -\frac{GM_Tm}{r^2} &= -m \frac{v^2}{r}\\ \frac{GM_T}{r^2} &= \frac{v^2}{r}\\ \frac{GM_T}{r} &= v^2\\ \end{split}

De acuerdo a la dinámica circular, podemos reescribir nuestra expresión teniendo en cuenta que la velocidad tangencial es igual a $v = r\omega$ donde $\omega = \frac{2\pi}{T}$ , siendo $T$ el periodo circular.

\begin{split} \frac{GM_T}{r} &= v^2\\ \frac{GM_T}{r} &= (r\frac{2\pi}{T})^2\\ \frac{GM_T}{r} &= r^2\frac{4\pi^2}{T^2}\\ T^2&= r^3\frac{4\pi^2}{GM_T}\\ \end{split}

Este último resultado corresponde a la Tercer ley de Keppler.